Учебник по физике для поступающих в ВУЗ
и минимальна Epmin = 0 в положении равновесия.
Кинетическая энергия, наоборот, минимальна Ekmin = 0 в точках поворота
и максимальна Ekmax = в положении равновесия.
Свободные колебания колебательной системы являются затухающими из-за наличия сил сопротивления (трения)
МАТЕМАТИЧЕСКИЙ МАЯТНИК (уч.10кл. стр.167-172)
Математический маятник.
Вынужденные и свободные колебания (см.выше уч.10кл.)
Свободные колебания пружинного маятника
График. Характер колебаний
Амплитуда. Формула
Период. Формула
Циклическая частота собственных гармонических колебаний пружинного маятника. Определение и формула
Полная механическая энергия свободных колебаний
Зависимость амплитуды от энергии
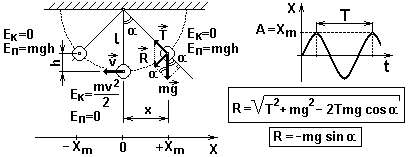
Тело небольших размеров, подвешенное на нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела, называется математическим маятником.
Математический маятник – это модель, реально таких маятников нет.
Вертикальное положением является положением равновесия, при котором сила тяжести уравновешивается силой упругости.
При малых отклонениях маятника от положения равновесия возникает равнодействующая сила, направленная к положению равновесия, и его колебания являются гармоническими.
Чтобы вывести эту формулу периода гармонических колебаний математического маятника, запишем второй закон Ньютона для маятника ΣFi = ma.
На маятник действуют сила тяжести и сила натяжения нити.
Их равнодействующая (см.рис.) равна: R = - mg
Следовательно, при малом угле отклонения (до 8о Rx ≈ R) по оси X:
max = mx’’ = - mg Þ x’’ + x = 0
Корни дифференциального уравнения ????
УТОЧНИТЬ ВЫВОД ФОРМУЛЫ ПЕРИОДА КОЛЕБАНИЙ
Откуда: ω =
Период гармонических колебаний математического маятника при небольшом угле размаха (до 8о) равен:
T = = 2π
При гармонических колебаниях тела, подвешенного на пружине, сила упругости равна по закону Гука: F = -kx.
Пусть: x(t) = A sin(ωt)
По второму закону Ньютона: -kx = ma
Учитывая, что ускорение a = dx2/dt2 = x’’ (вторая производная координаты по времени)
ma = mx’’ = -kx Þ -mω2Asin(ωt) = -kAsin(ωt) Þ
ω = , T = = 2π
ПЕРИОД КОЛЕБАНИЙ МАТЕМАТИЧЕСКОГО МАЯТНИКА (уч.10кл. стр.167-172)
См. выше «Математический маятник»
ПРЕВРАЩЕНИЯ ЭНЕРГИИ ПРИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЯХ
ДОБАВИТЬ
См.выше «Гармонические колебания», «Свободные колебания», «Математический маятник», «Резонанс»
При отклонении математического маятника от положения равновесия его потенциальная энергия увеличивается (увеличивается расстояние до Земли).
При движении к положению равновесия скорость маятника возрастает, и увеличивается кинетическая энергия, за счет уменьшения запаса потенциальной.
В положении равновесия кинетическая энергия – максимальная, потенциальная – минимальна. В положении максимального отклонения – наоборот.
С пружинным – то же самое, но берется не потенциальная энергия в поле тяготения Земли, а потенциальная энергия пружины.
Свободные колебания всегда оказываются затухающими, т.е. с убывающей амплитудой, т.к. энергия тратится на взаимодействие с окружающими телами.
Потери энергии при этом равны работе внешних сил за это же время.
Амплитуда зависит от частоты изменения силы.
Максимальной амплитуды она достигает при частоте колебаний внешней силы, совпадающей с собственной частотой колебаний системы.
Явление возрастания амплитуды вынужденных колебаний при описанных условиях называется резонансом.
Так как при резонансе внешняя сила совершает за период максимальную положительную работу, то условие резонанса можно определить как условие максимальной передачи энергии системе.
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ (уч.10кл. стр.167, 173-179)
Определение вынужденных колебаний (уч.10кл.стр.167)
Затухающие колебания. Определение. График для примера
Колебания под действием внешней силы (на примере)
Статическое смещение. Понятие
Определение вынужденных колебаний (уч.10кл.стр.177)
Вынужденные гармонические колебания тела. Закон колебаний. Формула амплитуды
Колебательная система.
Формула амплитуды вынужденных колебаний системы при наличии собственных колебаний
Резонанс
Свободные колебания колебательной системы являются затухающими. Однако на практике возникает потребность в создании незатухающих колебаний, когда потери энергии в колебательной системе компенсируются за счёт внешних источников энергии.
В этом случае в такой системе возникают вынужденные колебания.
Вынужденными называют колебания, происходящие под действием периодически изменяющегося воздействия, а сами воздействия — вынуждающими.
Вынужденные колебания происходят с частотой, равной частоте вынуждающих воздействий.
Амплитуда вынужденных колебаний возрастает при приближении частоты вынуждающих воздействий к собственной частоте колебательной системы. Она достигает максимального значения при равенстве указанных частот.
Явление резкого возрастания амплитуды вынужденных колебаний, когда частота вынуждающих воздействий равна собственной частоте колебательной системы, называется резонансом.
В реальной системе механическое движение всегда сопровождается трением. Силы трения, направленные противоположно перемещению маятника, совершают отрицательную работу, уменьшая его механическую энергию.
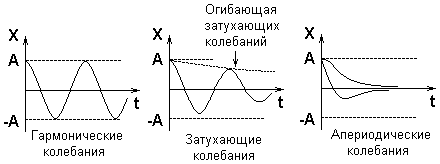
Затухающие колебания – колебания, амплитуда которых уменьшается с течением времени.
Апериодические колебания достигают установившегося значения за время меньше периода.
Статическое смещение – изменение положения равновесия колебательной системы под действием постоянной силы
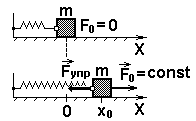
Fупр = kx0 = F0
Под действием F0 положение равновесия маятника смещается на
x0 = = (так как циклическая частота пружинного маятника ω0 = )
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
