Учебник по физике для поступающих в ВУЗ
Под действием э.д.с. самоиндукции создаётся индукционный ток, называемый током самоиндукции.
Если через соленоид протекает постоянный ток I = const, ЭДС самоиндукции отсутствует εsi = 0.
Так как катушка кроме индуктивного обладает и активным сопротивлением, то ток через нее: I = ε/R
Ток самоиндукции, согласно правилу Ленца, противодействует изменению силы тока в цепи, замедляя его возрастание или убывание.
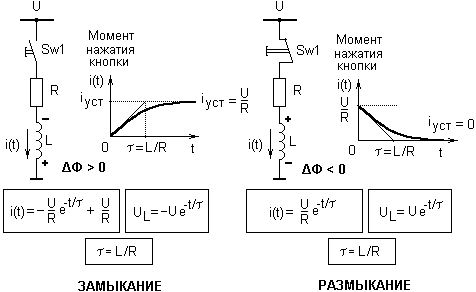
Особенно быстро сила тока изменяется при замыкании- размыкании (коммутации) цепи.
При замыкании кнопки магнитный поток соленоида начинает возрастать ΔΦ > 0. Согласно правилу Ленца, возникает индукционный ток, создающий индукцию направленную против внешнего поля. Полярность возникающей ЭДС самоиндукции, противоположной внешней ЭДС, препятствует нарастанию силы тока через катушку.
Реально ЭДС самоиндукции тормозит электроны в проводнике, из которого сделана катушка.
С течением времени, когда магнитный поток перестает изменяться (ΔΦ = 0), ЭДС самоиндукции становится равной нулю и устанавливается значение силы тока в контуре:
I = U/R.
При размыкании кнопки ток самоиндукции стремиться «поддержать» спадающий толк через катушку, и протекает в ту же сторону, в которую протекал ток в цепи до размыкания ключа. ЭДС самоиндукции поддерживает магнитный поток через катушку без изменений. Реально она ускоряет движение электронов в проводнике, из которого сделана катушка.
Поэтому в течении некоторого времени релаксации τL в разомкнутой цепи продолжает протекать ток самоиндукции.
Согласно закону Ома для L-R цепи:
isi = = -
Изменение тока в единицу времени:
i’ = = -
Величина –I в числителе характеризует полное изменение тока при размыкании.
Следовательно промежуток времени τL = L/R в знаменателе определяет по порядку величины время протекания тока размыкания, или время релаксации L-R цепи.
Время релаксации является характеристикой инерционных свойств любой электрической цепи.
В случае L-R цепи оно определяет как время протекания тока размыкания, так и время нарастания тока замыкания цепи.
Геометрически производная i’ характеризуется тангенсом угла наклона касательной к кривой тока i(t). При t = 0 касательная к графику i(t) пересекает ось t в точке τL. Так можно графически определить время релаксации.
Из-за большой индуктивности соленоида ЭДС самоиндукции может значительно превосходить ЭДС источника тока. Это приводит к перенапряжениям при размыкании цепи и возникновению электрической дуги (пробивание воздушного промежутка) между контактами.
Процесс самоиндукции задерживает увеличение и уменьшение тока в электрических схемах и линиях передачи сигналов, внося искажения в передаваемый сигнал.
Явление самоиндукции подобно инертности в механике. Тело нельзя ускорить или затормозить мгновенно, как бы не была велика ускоряющая или тормозящая сила, действующая на тело.
ИНДУКТИВНОСТЬ
Пусть по замкнутому контуру течёт постоянный ток силой I. Этот ток создаёт вокруг себя магнитное поле, которое пронизывает площадь, охватываемую проводником, создавая магнитный поток. Известно, что магнитный поток Ф пропорционален модулю индукции магнитного поля В, а модуль индукции магнитного поля, возникающего вокруг проводника с током, пропорционален силе тока 1.
Из этого следует: Φ = LI
Коэффициент пропорциональности L между силой тока и магнитным потоком, создаваемым этим током через площадь, ограниченную проводником, называют индуктивностью проводника.
Индуктивность контура – физическая величина, равная коэффициенту пропорциональности между магнитным потоком через площадь, ограниченную контуром проводника и силой тока в контуре.
Индуктивность проводника зависит от его геометрических размеров и формы, а также от магнитных свойств среды, в которой он находится.
Необходимо отметить, что если магнитная проницаемость среды, окружающей проводник, не зависит от индукции магнитного поля, создаваемого током, текущим по проводнику, то индуктивность данного проводника является постоянной величиной при любой силе тока, идущего в нём.
Это имеет место, когда проводник находится в среде с диамагнитными или парамагнитными свойствами.
В случае ферромагнетиков индуктивность зависит от силы тока, проходящего по проводнику.
В системе единиц СИ индуктивность измеряется Гн = Вб/А (Генри).
1 Гн — индуктивность такого проводника, при протекании по которому тока силой 1А возникает магнитный поток, пронизываю площадь, охватываемую проводником, равный 1Вб.
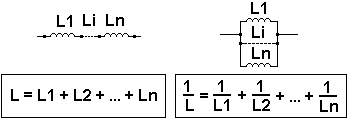
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
При протекании электрического тока по проводнику вокруг него возникает магнитное поле. Оно обладает энергией.
Если форма контура остается неизменной, то поток изменяется только за счет изменения силы тока DI:
DΦ =LDI
Выражение для элементарной работы при таком изменении силы тока имеет вид:
δA = LIDI
При изменении силы тока в проводнике от нуля до I суммарная работа определяется площадью под графиком Φ = LI:
A =
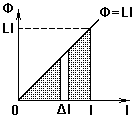
Такая же энергия магнитного поля накапливается в контуре с индуктивностью L при силе тока в нем I:
Wm =
Можно показать, что энергия магнитного поля, возникающего вокруг проводника с индуктивностью L, по которому течёт постоянный ток силой I, равна:
W =
Пусть при отключении катушки с индуктивностью L от источника, ток убывает по линейному закону. Тогда ЭДС самоиндукции имеет постоянное значение :
eis = - L=
За время t при линейном убывании в цепи пройдет заряд q = Iсрt = t
При этом работа электрического тока равна:
A = qeis = t * =
Эта работа совершается за счет энергии Wm магнитного поля катушки.
ДОБАВИТЬ ПРО ЭНЕРГИЮ МАГНИТНОГО ПОЛЯ ИЗ ДРУГОГО ИСТОЧНИКА
ИЗМЕРЕНИЕ СИЛЫ ТОКА, НАПРЯЖЕНИЯ, СОПРОТИВЛЕНИЯ ПРОВОДНИКА
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
