Учебник по физике для поступающих в ВУЗ
Мr =
Относительные атомные массы всех химических элементов точно измерены.
Складывая относительные атомные массы элементов, входящих в состав молекулы, можно вычислить относительную молекулярную массу вещества.
Количество вещества наиболее естественно измерять числом атомов или молекул, но их число очень велико. В расчетах используют не абсолютное число атомов или молекул, а относительное.
В Международной системе единиц количество вещества выражают в молях.
Единицей количества вещества является моль.
Моль – количество вещества, масса которого, выраженная в граммах, численно равна относительной атомной массе.
Моль равен количеству вещества системы, содержащей столько же частиц, сколько содержится атомов в 0,012 кг углерода.
Массу одного моля называют молярной массой и обозначают М
М= Мr * 1 г/моль
Единица молярной массы – кг/моль
Отношение числа молекул к количеству вещества называется постоянной Авогадро:
NA =
Постоянная Авогадро:
NA = 6.022*1023 моль-1
Она показывает, сколько атомов или молекул содержится в одном моле вещества.
Постоянная Авогадро одинакова для всех веществ, т.е. моль любого вещества содержит одинаковое число атомов (или молекул)
Постоянная Авогадро впервые была вычислена Перреном при опытах по изучению броуновского движения частиц.
Количество вещества можно найти как отношение числа атомов или молекул вещества к постоянной Авогадро:
υ =
Наряду с относительной молекулярной массой Mr в химии и физике широко используется понятие молярная масса вещества.
Молярной массой называется величина, равная отношению массы вещества к количеству вещества:
M =
Молярную массу можно выразить через массу молекулы:
M = m0NA
Масса вещества равна произведению массы одной молекулы на число молекул в теле:
m = m0N
Количество вещества равно отношению массы вещества к его молярной массе:
υ = = =
Для определения массы молекул нужно разделить массу вещества на число молекул в нем:
m0 = = =
ИЗМЕРЕНИЕ СКОРОСТИ МОЛЕКУЛ. ОПЫТ ШТЕРНА(уч.10кл.стр.236)
См. определение идеального газа (уч.10кл.стр.222,229- )
Статистические методы исследования идеального газа.
Распределение молекул идеального газа по скоростям
Опыт Штерна
Распределение молекул по скоростям в опыте Штерна (график и его объяснение)
Наиболее вероятная скорость молекул
Наиболее простой моделью является идеальный газ, состоящий из материальных точек, между которыми отсутствуют силы, действующие на расстоянии, и которые сталкиваются между собой как упругие шары.
Подобная модель одинакова для всех разряженных газов.
Свойства различных разряженных газов не зависят от взаимодействия между отдельными молекулами.
Информация об отдельной частице не представляет практического интереса для описания поведения газа как целого.
Статистическая закономерность в теории идеального газа – закон поведения совокупности большого числа частиц.
Микроскопические параметры – параметры малых масштабов (масса молекулы, ее скорость, импульс, кинетическая энергия), характеризуют движение отдельной молекулы.
Макроскопические параметры – параметры больших масштабов (масса газа, давление, объем, температура), характеризуют свойства газа как целого.
Молекулы идеального газа в отсутствии внешних сил равномерно распределены в пространстве.
Равномерное распределение в пространстве молекул идеального газа является его наиболее вероятным состоянием.
В результате хаотических столкновений молекулы идеального газа изменяют не только направление своего движения, но и скорость. Ответить сколько частиц обладают определенной скоростью невозможно.
Интерес представляет распределение молекул по скоростям.
В 1920 г. О.Штерн поставил опыт по определению скорости молекул газа или пара.
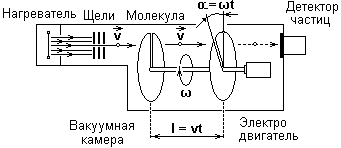
В нагревателе с поверхности серебряной проволоки, раскаленной электрическим током, испаряются атомы вещества. Попадая из нагревателя через отверстие в вакуумную камеру, молекулы пара с помощью системы щелей формируются в узкий пучок, направленный в сторону двух дисков, вращающихся с угловой скоростью ω. Диски используются для сортировки молекул по скоростям. Угол между прорезями в дисках α. Расстояние между дисками l в процессе эксперимента не изменяется.
Для того чтобы молекула пара (газа) попала на приемник детектора частиц, она должна пройти через прорези в дисках. Для этого время прохождения молекулы между дисками должно быть равно времени поворота прорези второго диска на угол α.
t = t = Þ v = ω
Угол прорезей ∆α в дисках конечен, поэтому через них будут проходить молекулы, скорость которых лежит в интервале от v до v + ∆v, где ∆v = v
Анализ данных опыта Штерна позволяет найти распределение молекул по скоростям.
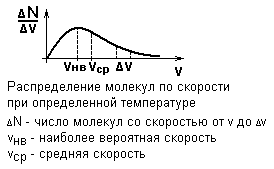
На графике изображена зависимость числа молекул, приходящихся на единичный интервал скоростей, от скорости, которой они обладают.
Максимум ∆N/∆v означает, что большинство молекул обладают такой скоростью.
Наиболее вероятная скорость – скорость, которой обладает максимальное число молекул.
Полученное распределение характерно для многих массовых процессов, характеризующихся внутренней неупорядоченностью, хаотичностью.
Выбирая определенный интервал скоростей ∆v, можно найти среднюю скорость молекул.
= =
Вычисления показывают, что средняя скорость молекул превышает наиболее вероятную.
> vн.в.
Скорость молекул газа:
Зная абсолютную температуру, можно найти среднюю кинетическую энергию молекул газа, а , следовательно, и средний квадрат их скорости.
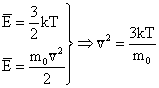
Квадратный корень из этой величины называется средней квадратичной скоростью:
=
Опыты по определению скоростей молекул доказали справедливость этой формулы.
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
