Учебник по физике для поступающих в ВУЗ
где U = φ1 – φ2 - разность потенциалов в начальной и конечной точках траектории.
Разность потенциалов (напряжение) между двумя точками равна отношению работы поля по перемещению заряда из начальной точки в конечную к этому заряду:
U = φ1 – φ2 =
Единица измерения – В (Вольт) В =
Разность потенциалов обычно называют напряжением и обозначают U.
Aq = qU
Разность потенциалов (напряжение) между двумя точками численно равна работе сил электростатического поля при перемещении единичного положительного заряда из начальной точки в конечную.
А+1 = U (Дж)
1 В – разность потенциалов двух точек электростатического поля, при перемещении между которыми заряда 1 Кл поле совершает работу в 1 Дж.
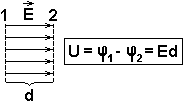
Разность потенциалов между двумя точками, находящимися на расстоянии d друг от друга в однородном электростатическом поле вдоль линий напряженности:
U = Ed
Разность потенциалов между точками 1 и 2, находящимися на расстояниях r1 и r2 от точечного заряда +Q:
U = ( - )
Электрометр
Разность потенциалов измеряют электрометром – электроскопом с металлическим корпусом.
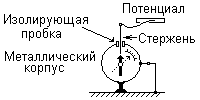
Основная его часть – легкая аллюминиевая стрелка, укрепленная на металлическом стержне с помощью горизонтальной оси.
Центр тяжести стрелки находится ниже оси, так что до начала измерений стрелка находится вертикально.
Стержень со стрелкой помещен в металлический корпус и изолирован от него эбонитовой пробкой.
Для измерения разности потенциалов между двумя проводниками один из них присоединяют к стержню электрометра, а другой – к его корпусу.
Если хотят измерить потенциал относительно земли, то корпус электрометра заземляют.
Электрическое поле внутри электрометра, а следовательно и угол поворота стрелки, зависит только от разности потенциалов между стержнем и корпусом, так как внешнее электрическое поле заряженных или поляризованных тел не проникает через металлический корпус прибора.
Для градуирования прибора его подсоединяют к проводникам, напряжения между которыми известны.
С помощью электрометра легко убедиться, что все точки проводника имеют одинаковый потенциал относительно земли.
ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ(уч.10кл.стр.368-375)
Напряженность электростатического поля (см.выше уч.10кл.стр.363-365)
Линии напряженности поля (см.выше уч.10кл.стр.366-368)
Напряженность поля системы зарядов
Принцип суперпозиции полей
Использование принципа суперпозиции для построения линий напряженности системы зарядов
Электрическое поле диполя.
Определение диполя.
Определение плеча диполя
Напряженность точки в поле диполя
Электростатическое поля заряженной сферы
Область сосредоточения поля сферы
Формула напряженности поля сферы (уч.10кл.стр.374)
Понятие, формула и единицы измерения поверхностной плотности заряда (уч.10кл.стр.374)
Электрическое поле заряженной плоскости
Силы действующие на единичный положительный заряд в данной точке со стороны других зарядов, не зависят друг от друга.
Принцип суперпозиции электрических полей
Напряженность поля системы зарядов в данной точке равна геометрической (векторной) сумме напряженностей полей, созданных в этой точке каждым зарядом в отдельности.
![]()
Согласно принципу суперпозиции действия сил результирующая сила F действующая на единичный положительный заряд q0 равна геометрической сумме всех кулоновских сил действующих на него со стороны других зарядов:
![]()
Разделив обе части на q0 получим (учитывая, что ![]() ) математическую запись принципа суперпозиции электрических полей:
) математическую запись принципа суперпозиции электрических полей:
![]() Þ
Þ![]()
Принцип суперпозиции позволяет рассчитать напряженность поля произвольной системы зарядов.
Пример – напряженность поля двух точечных зарядов:
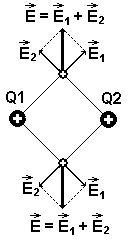
Систему зарядов с суммарным зарядом Q ≠ 0 на расстоянии много больше размера системы можно рассматривать, как точечный заряд. Напряженность ее поля на таком расстоянии будет как и у точечного заряда:
E ≈
Для системы зарядов с суммарным зарядом Q = 0 напряженность поля на расстоянии много большем размеров системы не равна нулю.
Покажем это на примере электрического диполя.
Электрический диполь – система, состоящая из двух равных по модулю разноименных точечных зарядов.
Плечо диполя – отрезок прямой, соединяющий заряды.
В качестве диполя можно рассматривать любую полярную молекулу HCl, CuCl2.
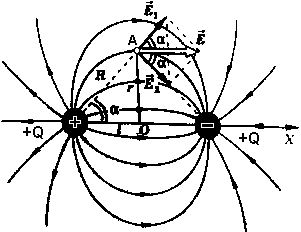
Пусть l – плечо диполя
Напряженность в точке А, находящейся на одинаковом расстоянии от зарядов:
E1 = E2 = ; R2 = r2 + (l/2)2 Þ E1 = E2 =
По принципу суперпозиции полей ![]()
Суммарная напряженность поля направлена параллельно оси диполя по оси Х.
Ex = E1x + E2x
E1x, E2x - проекции напряженностей на ось Х
Из рисунка видно, что
E1x = E2x = E1 cos(a) ; cos(a) = =
E1 = E2 = ; Ex = E1x + E2x Þ E = k
Так как r >> l, то можно пренебречь l по сравнению с r,
напряженность поля на большом расстоянии от диполя:
E ≈ k ≠ 0
E ≈ k = (k )
k – напряженность поля точечного заряда
– характеризует малость результирующей напряженности диполя по сравнению с напряженностью поля точечного заряда.
Поле диполя мало из-за компенсации полей разноименных зарядов. На большом расстоянии от диполя напряженность убывает по закону 1/r3, т.е гораздо быстрее, чем в случае точечного заряда (1/r2).
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
