Учебник по физике для поступающих в ВУЗ
Число линий, пронизывающих единицу площади, характеризует модуль напряженности поля.
Пусть для точечного положительного заряда +Q сквозь единицу поверхности сферы радиуса r вокруг заряда проходит N линий напряженности. Степень сгущения составляет:
~
Напряженность Е так же пропорциональна , значит E ~
Модуль напряженности поля пропорционален степени сгущения линий напряженности электростатического поля.
В области сгущения линий напряженности больше, в области разряжения – меньше.
Если расстояние между линиями напряженности одинаково (линии параллельны), то одинакова и напряженность поля.
Электрическое поле, векторы напряженности которого одинаковы во всех точках пространства, называется однородным.
В ограниченной области пространства электрическое поле можно считать приблизительно однородным, если напряженность поля внутри области меняется незначительно.
см. ниже «Диэлектрическая проницаемость» (уч.10кл.390-391)
Относительная диэлектрическая проницаемость среды – число, показывающее во сколько раз напряженность электростатического поля в однородном диэлектрике меньше, чем напряженности в вакууме:
e =
Обозначение - e
Следовательно, напряженность поля в диэлектрике:
E =
Напряженность электрического поля зависит от относительной диэлектрической проницаемости среды e поэтому при наличии нескольких граничащих диэлектриков на границе разрыва двух сред напряженность поля меняется скачком (линии вектора Е терпят разрыв).
Электрическое смещение
Электрическое смещение D в данной точке среды – векторная величина, численно равная произведению относительной диэлектрической проницаемости среды, электрической постоянной на напряженность поля в данной точке.
![]()
![]()
![]() = ee0
= ee0![]()
Единица измерения D - Кл/м2
Вектор D не зависит от e:
Для точечного заряда или заряженной сферы:
E = Þ D = ee0=
Для заряженной плоскости:
E = Þ D = ee0 =
Вектор электрического смещения D не зависит от относительной диэлектрической проницаемости среды e, т.е. является одинаковым по величине во всех средах, поэтому не имеет скачка и разрыва на границе сред. (в отличие от напряженности Е)
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ТОЧЕЧНОГО ЗАРЯДА(уч.10кл.стр.363-365, 366-368)
Напряженность электростатического поля (см.выше уч.10кл.стр.363-365)
Линии напряженности электростатического поля (см.выше)
Линии напряженности поля единичного заряда (положительного и отрицательного)
Сгущение линий напряженности поля (см.выше)
Понятие однородного электрического поля (см.выше)
Напряженность электрического поля сферы (см.ниже уч.10кл.стр.374)
ПОТЕНЦИАЛЬНОСТЬ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ(уч.10кл.стр.378-381)
Аналогия движение частицы в гравитационном и электростатическом полях
Работа сил электростатического поля при перемещении частицы в нем
Потенциальность электростатического поля.
Обозначение потенциальной энергии электростатического поля
Потенциальная энергия взаимодействия точечных зарядов. Формула(уч.10кл.стр.380)
Знаки в выражении для энергии взаимодействия поля и их физический смысл
Работа в гравитационном поле Ag = mgh
Работа в электростатическом поле Aq = Fkh = qEh
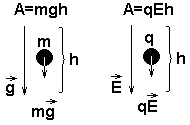
Движение частицы в гравитационном поле аналогично ее движения в электростатическом. В первом случае фигурирует сила mg, во втором – кулоновская сила qE
Силы гравитационного и электростатического полей зависят от 1/r2 и направлены по прямой соединяющей тела.
Fg = G
F-q =
При перемещении заряда действующая на него со стороны поля сила совершает работу.
Поэтому можно утверждать, что заряженное тело в электрическом поле обладает энергией.
Найдем потенциальную энергию по перемещению заряда в однородном электрическом поле. Однородное поле создают, например, большие металлические пластины, имеющие заряды противоположного знака.
Такое поле действует на заряд с постоянной силой:
![]()
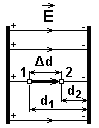
Вычислим работу поля при перемещении положительного заряда q из точки 1, находящейся на расстоянии d1 от пластины, в точку 2, расположенную на расстоянии d2< d1 от той же пластины. Точки 1 и 2 лежат на одной силовой линии.
На участке Dd = d1 – d2 электрическое поле совершит положительную работу:
A = qE (d1 – d2) = - (qEd1 – qEd2)
Эта работа не зависит от формы траектории.
Если работа не зависит от формы траектории, то она равна изменению потенциальной энергии, взятому с противоположным знаком:
A = - (Wp1 – Wp2) = - DWp
Сравнивая полученные выражения, видим, что потенциальная энергия заряда в однородном электростатическом поле:
Wp = qEd
На замкнутой траектории, когда заряд возвращается в начальную точку, работа поля равна нулю:
A = - DWp = - (Wp1 – Wp1) = 0
Работа сил электростатического поля при перемещении заряженной частицы из одной точки поля в другую не зависит от формы траектории, а зависит лишь от начального и конечного положения частицы.
Электростатическое поле потенциально
Силы электростатического поля консервативны - их работа не зависит от траектории движения.
Работа сил электростатического поля равна разности потенциальных энергий заряженной частицы в начальном и конечном положениях:
A = Wp1 – Wp2
Физический смысл имеет не сама потенциальная энергия, а разность ее значений, определяемая работой поля при перемещении заряда из начального положения в конечное:
Wp = qEd1 – qEd2
Точка отсчета потенциальной энергии электростатического поля выбирается произвольно.(Обычно на бесконечности)
Обычно нуль отсчета потенциальной энергии выбирается на бесконечно большом расстоянии, где заряды практически не взаимодействуют друг с другом.
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
