Учебник по физике для поступающих в ВУЗ
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ (уч.10кл. стр.135-142, 153)
Определение потенциальной силы
Работа потенциальной силы
Определение потенциальной энергии
Работа сил трения, тяжести га примере скатывания тела по наклонной плоскости
Принцип минимума потенциальной энергии
Устойчивое, неустойчивое, безразличное равновесия. Определения и примеры
Работа силы тяжести (уч.10кл.стр.139)
Потенциальная энергия в гравитационном поле. Формула
Работа силы тяжести в гравитационном поле
Зависимость потенциальной энергии в поле тяжести от расстояния до центра поля. График
Работа силы упругой деформации
Потенциальная энергия тела при упругом взаимодействии. Формула
Зависимость потенциальной энергии упругой деформации от деформации. График
Упругое и не упругое столкновение. Определения. Переход энергии. (уч.10кл.стр.153)
Закон сохранения полной механической энергии изолированной системы (коротко)
Потенциальная(Консервативная) сила – сила, работа которой при перемещении материальной точки зависит только от начального и конечного положений точки в пространстве.
Работа консервативной силы при перемещении материальной точки по замкнутому контуру равна нулю.
Например, сила тяжести – потенциальная сила, ее работа не зависит от формы траектории (см. выше сила тяжести)
Потенциальной (лат. потенция – возможность) энергией называется энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.
Потенциальная энергия тела в данной точке – скалярная физическая величина, равная работе, совершаемой потенциальной силой при перемещении тела из этой точки в точку, принятую за нуль отсчета потенциальной энергии.
Единица измерения – Дж (Джоуль)
Обозначение - Еp
Потенциальной энергией обладает всякое упруго деформированное тело.
Потенциальную энергию сжатого газа используют в тепловых двигателях, пневмоинструменте и т.д.
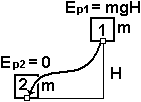
Так работа силы тяжести Ag = Ep1 – Ep2 = mgH
Потенциальная энергия в этом случае характеризует энергию гравитационного притяжения материальной точки к Земле.
Потенциальная энергия материальной точки, поднятой на высоту Н над «нулем»
Eр = mgH
Потенциальная энергия зависит от координаты (относительно «нуля» потенциальной энергии)
Изменение потенциальной энергии характеризует работу силы тяжести по перемещении тела. Эта работа равна изменению потенциальной энергии, взятому с противоположным знаком. Тело находящееся ниже поверхности земли, имеет отрицательную потенциальную энергию.
В общем случае работа всех сил, действующих на тело равна сумме работ потенциальных и не потенциальных сил: A = Ap + Anp
Принцип минимума потенциальной энергии:
Любая замкнутая система стремиться перейти в такое состояние, в котором ее потенциальная энергия минимальна.
Устойчивое равновесие – равновесие, при котором тело, выведенное из положения равновесия, возвращается в первоначальное положение.
Неустойчивое равновесие – равновесие, при котором тело, выведенное из положения равновесия, не возвращается в первоначальное положение.
Безразличное равновесие – равновесие, при котором соседние положения тела также являются равновесными.
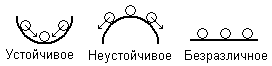
Работа силы тяжести при перемещении тела на высоту Н:
Fg = - G
Ag = FgH cos(0) = G H
Ag = Ep(r) – Ep(r-H)
Потенциальная энергия тела массой m в гравитационном поле:
Ep(r) = - G
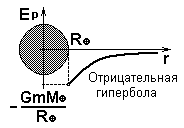
Начало отсчета находится на бесконечно большом расстоянии от Земли (на бесконечности) На этом расстоянии стремиться к нулю и сила гравитационного притяжения к Земле
Расстояние во всех инерциальных системах отсчета одно и тоже. Поэтому потенциальная энергия не зависит от выбора системы отсчета, а зависит от выбора «нуля» отсчета.
Работа силы упругости при растяжении и сжатии пружины
Потенциальную энергию имеют не только поднятые тела. Рассмотрим работу, совершаемую силой упругости при деформации пружины.
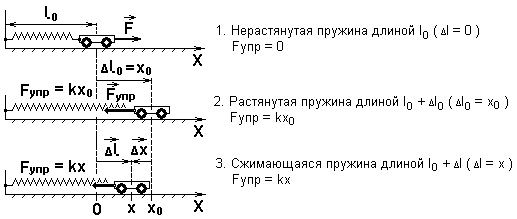
Сила упругости меняется от Fупр = kx0 до Fупр = kx
Средняя сила упругости Fупр.ср = = (x0 + x)
Направление средней силы упругости ![]() и перемещения
и перемещения ![]() совпадают
совпадают
Работа силы упругости зависит только от начального и конечного положений.
Это значит, что сила упругости - потенциальна.
Aупр = (x0 + x)∆x = (x0 + x)(x0 - x) = -
Потенциальная энергия пружины (упругодеформированного тела)
Ep =
x – удлинение или сжатие тела (пружины)
k – жесткость тела (пружины)
Начало отсчета соответствует нерастянутой пружине, удлинение которой x=0
Потенциальная энергия упругодеформированной пружины равна работе силы упругости при переходе пружины из деформированного состояния в недеформированное.
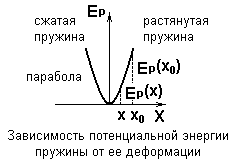
Потенциальная энергия упругодеформированной (сжатой или растянутой) пружины зависит от степени ее деформации.
Важной характеристикой потенциальной энергии является то, что тело не может обладать ею, не взаимодействуя с другими телами.
Потенциальная энергия характеризует взаимодействующие тела, кинетическая – движущиеся. И та, и другая возникают в результате взаимодействия тел.
Если тела взаимодействую между собой только силами тяготения и силами упругости, и никакие внешние силы на них не действуют (или же их равнодействующая равна нулю), то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии, взятой с противоположным знаком.
В то же время, по теореме о кинетической энергии (изменение кинетической энергии тела равно работе внешних сил) работа тех же сил равна изменению кинетической энергии:
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
