Теория поля
Векторное произведение будем обозначать символом 
Модуль векторного произведения
Если поменять местами вектора, то получим
т.е.
векторное произведение не коммутативно.
Согласно вышеизложенному для векторного произведения ортов правой прямоугольной системы координат имеем:
Используя эти формулы, найдем выражение для векторного произведения векторов А и В через проекции сомножителей:
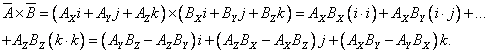
Очень удобно векторное произведение записывать в таком виде:
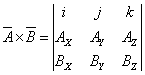
Для векторного произведения справедлив распределительный закон:
- Чему равно двойное векторное произведение?
Три вектора 
и 
можно различным образом перемножить. Одним из этих вариантов и является двойное векторное произведение, т.е. вектор 
умножить векторно на .
Двойное векторное произведение 
Векторное произведение вектора 
на вектор 
представляет собой вектор, компланарный с векторами и и перпендикулярный вектору .
Найдем проекции вектора 
на ось х:
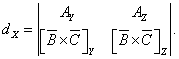
Раскрывая определитель, прибавим к правой части, а затем вычтем из нее 
Ах Вх Сх , после преобразований получим:
Для двух других проекций находим:
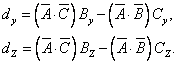
На основании этих формул запишем векторное равенство:
Произведение четырех и более векторов можно свести к произведению трех векторов.
- Как дифференцируется векторная функция?
- Дифференциал векторной функции 
является векторной величиной:
.
Значение дифференциала зависит от знака приращения независимой переменной dt . При 
вектор 
направлен по касательной к годографу в сторону возрастания аргумента t, при dt<0 направлен обратно.
Пусть дан радиус-вектор 
точки
,
дифференциал его определяется формулой
.
Модуль дифференциала описывается формулой:
Сравнив модуль дифференциала радиуса-вектора точки с дифференциалом дуги кривой ds:
получим:
- Как находится неопределенный интеграл векторной функции? Определенный интеграл?
- Неопределенный интеграл есть векторная функция 
, производная от которой равна подынтегральной функции:
.
Определенный интеграл от векторной функции есть предел суммы векторов:
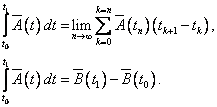
1.2. Основные характеристики скалярных и векторных полей. Графическое изображение полей. Уровенные поверхности, векторные линии и трубки. Градиент скалярного поля. Скорость изменения скалярного поля по заданному направлению. Выражение площади через вектор. Поток вектора через поверхность. Дивергенция вектора. Соленоидальные поля. Формула Остроградского-Гаусса. Циркуляция вектора. Ротор. Потенциальные поля. Формула Стокса. Оператор Гамильтона. Дифференциальные операции второго порядка, лапласиан.
- Как графически изображаются скалярные и векторные поля?
- Скалярные и векторные поля удобно изображать графически. Скалярное поле может быть изображено при помощи поверхностей уровня, т.е. поверхностей, во всех точках которых функция 
или 
сохраняет одинаковое значение.
Уравнение поверхности уровня или изоповерхности имеет вид:
Различные значения с соответствуют различным уровенным поверхностям. Совокупность таких поверхностей позволяет наглядно представить скалярное поле.
Перейти на страницу: 1 2 3 4 5 6 7 8