Фонон
Из (2) для амплитуды Cn получаем уравнение:
|
|
(6) |
Эти уравнения образуют бесконечную систему линейных уравнений. Если применить к цепочке граничные условия Борна-Кармана, то система будет конечной. (Заметим, что условия Борна-Кармана в одномерном случае эквивалентны тому, что цепочка достаточно большой длины L замкнута в кольцо). Тогда, приравняв определитель нулю, можно найти частоты колебаний, а затем, решив систему уравнений для каждой из найденных частот — соответствующие амплитуды.
Но мы поступим иначе. Будем искать решение в виде плоской волны:
|
|
(7) |
Подставив это выражение в (6), получим:
|
|
(8) |
Разделим последнее уравнение на exp(ikxn) и воспользуемся тем, что xn+1 = xn+a, xn–1 = xn–a:
|
–Mω2 = γ(eika+e–ika–2) |
(9) |
Таким образом, подстановка в виде плоской волны оказалась верной: мы избавились от номера атома n и получили уравнение, связывающее ω и k, т. е. уравнение, определяющее закон дисперсии волн.
Поскольку
|
|
(10) |
то
|
|
(11) |
и мы получаем закон дисперсии для упругих колебаний одномерной цепочки:
|
|
(12) |
Итак, мы пришли к выводу, что смещения атомов при колебании одномерной цепочки описываются плоской гармонической волной:
|
|
(13) |
Точнее, колебания представляют собой произвольную сумму таких волн. Здесь φ — фаза комплексной амплитуды A: A = |A|exp(iφ).
Напомним, что смещение — вещественная величина, которая описывается вещественной частью комплексной плоской гармонической волны, что явно записано в (13). В дальнейшем, при описании вещественных колебаний комплексной плоской волной, мы будем для краткости опускать обозначение вещественной части.
Волновой вектор k в плоской волне (13) может, вообще говоря, быть любым. Но вследствие дискретности цепочки (xn может принимать лишь дискретный набор значений na) плоские волны, волновые вектора которых отличаются друг от друга на произвольный вектор обратной решетки 2π l/a, описывают одно и то же колебание. (Здесь l — любое целое число).
Действительно, т. к. xn = na, то
|
|
(14) |
Поэтому достаточно рассматривать волновые вектора, лежащие в первой зоне Бриллюэна –π/a<k<π/a. Крайние значения волнового вектора ±π/a соответствуют одному и тому же колебанию с минимальной длиной волны λ = 2π/k = 2a. При такой длине волны соседние атомы цепочки движутся в противофазе. Интуитивно ясно, что короче длина волны быть уже не может.
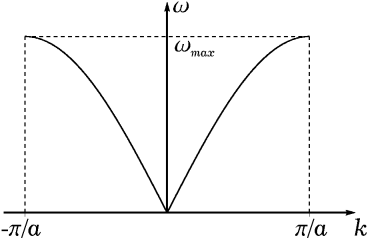
График зависимости ω(k) для одномерной цепочки с одним атомом в примитивной ячейке изображен на рис. 2.
|
Рис. 2. Закон дисперсии колебаний цепочки с одним атомом в примитивной ячейке. |
Обсудим теперь особенности закона дисперсии (12).
Важным его свойством является то, что частота волн, распространяющихся по цепочке, ограничена частотой ![]() . Чтобы оценить эту частоту, надо знать порядок величины постоянной γ.
. Чтобы оценить эту частоту, надо знать порядок величины постоянной γ.
Посмотрим на размерность γ. Сила F равна произведению γ на смещение u, поэтому:
|
|
(15) |
Характерная длина, межатомное расстояние a, имеет порядок 1A = 10–8 cм. Характерная энергия — энергия, которую приобретает атом при смещении на расстояние порядка a. Ее можно оценить как энергию химической связи, которая по порядку величины равна 10 эВ. Таким образом,
|
|
(16) |
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13