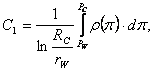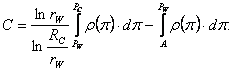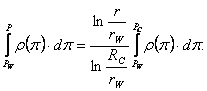или, после деления на 2b и переноса в другую часть равенства ::: physicedu.ru

Фильтрация газов - Дипломная работа

Страница 7

или, после деления на 2b и переноса в другую часть равенства:

где – функция, линейная относительно и’x , u’h , u (см. выше, формула (1.4.5)).

Полученное уравнение имеет более простой вид, чем исходное уравнение (1.4.1); если мы его сможем решить (т. е. найти и как функцию от x и h), то для того, чтобы найти решение исходного уравнения, достаточно вернуться к старым переменным (выразив x и h через х и у).

1.5. Выводы

В данной главе представлены основные уравнения состояния реального газа, уравнения, описывающие процесс фильтрации газа в пористой среде. Дано описание задачи. Сформулированы физическая и математическая постановки температурной и гидродинамической задач. Описан метод характеристик, который использован для получения решения задачи в главе 2.

Глава 2. Аналитическое решение задачи о баротермическом эффекте с учетом реального уравнения состояния

В данной главе приведены аналитические решения гидродинамической и температурной задач для произвольного уравнения состояния.

2.1. Решение гидродинамической задачи

Решение уравнения (I.4.1.1) приводит к необходимости решения дополнительной гидродинамической задачи для отыскания поля давления. Для описания движения газа воспользуемся квазистационарным уравнением неразрывности:

(2.1.1)

Скорость фильтрации газа сквозь пористую среду определяется законом Дарси:

(2.1.2)

Здесь - проницаемость пористой среды, - вязкость газа. Полагая, что и не меняются при движении газа к скважине, и что плотность газа зависит только от давления (баротропное приближение), перепишем уравнение неразрывности в следующем виде:

(2.1.3)

Функцию Лейбензона представим в виде:

(2.1.4)

где величины и А задаются граничными условиями. Подставляя функцию Лейбензона в уравнение (2.1.3), получим:

(2.1.5)

Учитывая, что для осесимметричного течения поле давлений является функцией координаты , уравнение (2.1.5) можно представить в виде:

(2.1.6)

Решение этого уравнения представим в виде:

(2.1.7)

где и - постоянные интегрирования, определяемые граничными условиями. Пусть - давление на границе контура питания (при ), - давление в скважине (при ), тогда согласно (2.1.4) и (2.1.7)