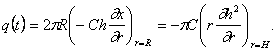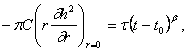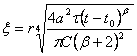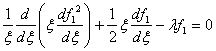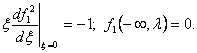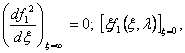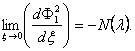Физическое описание явления фильтрации жидкости
(93)
где r - расстояние рассматриваемой точки пласта от оси симметрии.
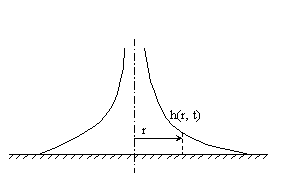 Рассмотрим следующую задачу. Пусть в бесконечный пласт, ограниченный снизу непроницаемой горизонтальной поверхностью - водоупором, через скважину, радиус которой пренебрежимо мал, начинается закачка жидкости. Предположим, что начальный напор жидкости в пласте равен нулю, так что начальное условие на бесконечности имеют вид:
Рассмотрим следующую задачу. Пусть в бесконечный пласт, ограниченный снизу непроницаемой горизонтальной поверхностью - водоупором, через скважину, радиус которой пренебрежимо мал, начинается закачка жидкости. Предположим, что начальный напор жидкости в пласте равен нулю, так что начальное условие на бесконечности имеют вид:
h(r, t0) = 0; h(¥, t) = 0. (94)
Предположим далее, что расход закачиваемой жидкости изменяется со временем по степенному закону. Выражение для полного расхода жидкости, закачиваемой через скважину радиусом R, имеет вид:
|
(95)
По предположению, радиус скважины пренебрежимо мал (ниже мы остановимся на причинах, по которым это допущение можно делать для большинства реальных движений), поэтому можно принять R = 0; так как расход жидкости, закачиваемой в скважину, меняется по степенному закону, граничное, условие на скважине принимает вид:
|
(96)
|
|
(97)
Здесь
(98)
представляют собой две независимые безразмерные комбинации определяющих параметров решения; других независимых комбинаций этих параметров не существует. Постоянный множитель снова введен в формулу для x с целью удобства последующего изложения. Как и прежде, искомая функция должна быть непрерывной и иметь непрерывную производную от квадрата. Подставляя выражение (77) в уравнение (93) и условия (94) и (96), находим, что функция f1 (x, l) удовлетворяет уравнению
|
(99)
при условиях
|
(100)
Исследование этой граничной задачи проводится аналогично предыдущему; также единственным образом строится функция f1 (x, l), отличающаяся от нуля лишь при 0 £ x £ x1(l), где x1 (l) - некоторая функция x, а при x ³ x1 (l) тождественно равная нулю. Функция f1 (x, l) при x®0 имеет особенность, как нетрудно видеть из первого условия (100):
|
(101)
Второе условие (100) может быть приведено к другой форме: умножая уравнение (99) на x и интегрируя в пределах от x = 0 до x = ¥, получаем, используя оба условия (100) и условия
|
(102)
|
(103)
Первое условие (102) непосредственно следует из условия, которому функция f1 (x, l) на бесконечности, так как если бы предел == при x ® ¥ не был равен нулю, то функция f1 (x, l) не стремилась бы к нулю при x ® ¥. Второе условие (102) непосредственно следует из (101).
Эффективное вычисление функции f1 (x, l) удобно проводить следующим образом. Строим решение задачи Коши Ф1(x, l) для уравнения (99). обращающееся в нуль при x = 1 и имеющее в этой точке конечную первую производную. Исследование, в точности аналогичное приведенному в п. 3 x1, показывает, что эта производная равна -1/4. Строить решение задачи Коши удобно так: вблизи x = 1 можно представить решение в виде ряда, при помощи которого находится надлежащее число начальных значений, после чего применяется метод численного интегрирования Адамса - Штермера. Далее численно вычисляется величина
|
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15