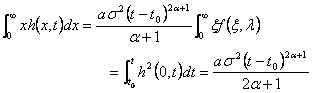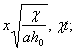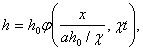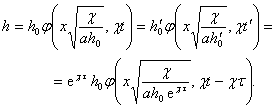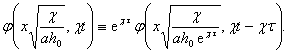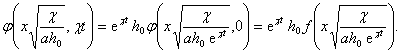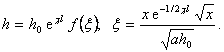Физическое описание явления фильтрации жидкости
Интегрируя это соотношение в пределах от t = t0 до t и используя граничное условие (61) и представление решения (66), имеем
|
(напомним, что считаем a удовлетворяющим неравенству -1/2<a< ¥), откуда получаем искомое условие в форме
|
(71)
В интересующей нас области изменения a и l правая часть (71) конечна и положительна.
3.2. ПОЛОГИЕ БЕЗНАПОРНЫЕ ДВИЖЕНИЯ
С НУЛЕВЫМ НАЧАЛЬНЫМ НАПОРОМ:
ПРЕДЕЛЬНЫЕ АВТОМОДЕЛЬНЫЕ ДВИЖЕНИЯ,
ОСЕСИММЕТРИЧНЫЕ АВТОМОДЕЛЬНЫЕ ДВИЖЕНИЯ
3.2.1. Предельные автомодельные движения. Рассмотрим теперь для того же полубесконечного пласта несколько иную задачу. Будем исследовать движение на полубесконечном интервале времени (-¥, t), поэтому начальное распределение напора по пласту несущественно.
Предположим, что на больших расстояниях от границы пласта, т.е. при х® ¥, напор жидкости равен нулю; следовательно,
h(¥, t) = 0. (72)
Пусть, далее, напор жидкости на границе пласта возрастет со временем по экспоненциальному закону:
h(0, t) = h0eht. (73)
Напор жидкости внутри пласта h(x, t) по-прежнему удовлетворяет уравнению
|
(74)
Составим полный список аргументов, от которых зависит это решение. Помимо координаты х и времени t, в этот список войдут также величины h0, == и a. Тогда размерности всех определяющих параметров решения представляются в виде:
[x]=L; [t]=T; [a]=[h]-1L2T-1; [h0]=[h]; [c]=T-1, (75)
где по-прежнему символы L, T и [h] означают соответственно размерности длины, времени и напора. Из пяти аргументов (75) с тремя независимыми размерностями можно составить две независимые комбинации, которые удобно взять в виде:
|
|
(76)
где j - безразмерная функция.
Положим теперь t = t¢ + t , где t - произвольная константа. При этом условие (72) и уравнение (74), как нетрудно проверить, записываются через новую переменную t¢, так же как и через прежнюю переменную, а условие (73) принимает вид:
|
Таким образом, сдвиг во времени влияет лишь на некоторое преобразование величины h0, и постановка задачи оказывается по отношению к группе преобразований переноса по времени; для определения h в переменных х, t¢, a, c, h¢0 получается та же задача, что и для определения h в переменных (75). Стало быть, на основе соотношений (76) и (77) имеем
|
(78)
|
(79)
Положим теперь t = t и получим
|
Итак, функция h, зависящая от пяти аргументов (75), представляется через функцию одного аргумента:
|
(81)
Подставляя (81) в основное уравнение (74), получаем для функции f(x) обыкновенное дифференциальное уравнение
|
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15