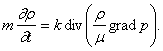Физическое описание явления фильтрации жидкости
|
Представляя (45) в (44), имеем
|
(46)
В это уравнение следует подставить соотношение
H(x, y, t) = h(x, y, t) + h0 (x,y),
определяющее вертикальную координату свободной поверхности Н через ее расстояние h до водоупора и расстояние h0 от водоупора до плоскости отсчета z = 0; получим окончательное уравнение для определения h. В частности, если поверхность водоупора представляет собой горизонтальную плоскость, то ее можно принять за плоскость отсчета и, следовательно, h0 (x,y) можно считать равным нулю. Тогда Н= h, и уравнение (46) принимает вид:
|
(47)
Уравнения (46) и (47) были даны Буссинеском.
2.4. Основные уравнения фильтрации газа
При исследовании фильтрации газа основное значение имеет тот факт, что сжимаемость газа обычно на несколько порядков превышает сжимаемость пористой среды. С учетом этого обстоятельства в уравнении неразрывности
|
(48)
изменением пористости m во времени можно пренебречь, так что получим
|
(49)
Для того чтобы получить замкнутую систему уравнений, снова нужно использовать связь плотности газа r с его давлением р и температурой Т:
r = r(р,Т), (50)
поэтому в задаче появляется новая переменная Т, и для замыкания системы уравнений нужно добавить еще одно уравнение - уравнение энергии. Однако, если в среде отсутствуют источники выделения или поглощения энергии, то изменения температуры в процессе движения газа крайне малы, и при расчете поля давления газа ими можно пренебречь. Это обстоятельство легко понять, если учесть, во-первых, крайнюю малость скорости фильтрации и, во-вторых, наличие теплового балласта - скелета пористой среды, эффективно подавляющего изменения температуры. Будем поэтому считать, что
r = r(р,Т0)= r(р), (51)
где Т0 - постоянная температура.
Присоединяя к уравнениям (49) и (51) уравнение закона фильтрации (предполагаемого линейным)
|
(52)
получаем замкнутую систему уравнений. Исключая скорость фильтрации, имеем
|
(53)
В уравнении (53) r - известная функция давления. Аналогично и вязкость газа, зависящая в общем случае от давления и температуры, может быть представлена в виде:
m = m(р,Т0) =m(р). (54)
Таким образом, и вязкость может считаться известной функцией одного лишь давления.
Введем теперь функции
|
(55)
Уравнение (53) принимает при этом вид:
|
(56)
Можно показать, что уравнение для давления сохранит форму (56) и в случае, если учитывается деформируемость пористой среды, т. е. зависимость от давления пористости и проницаемости (среда по-прежнему считается однородной).
В простейшем случае, когда газ можно считать термодинамически идеальным, с вязкостью, не зависящей от давления,
|
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15