Упругие волны
Значение производной в сечении x+δ можно для малых δ представить с большой точностью в виде
 |
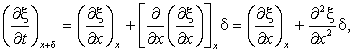где под подразумевается значение второй частной производной ξ по х в сечении х.
Ввиду малосги величин Δx, ξ и Δξ произведем в выражении (5.3) преобразование (5.4):
 |
|
|
(относительное удлинение при упругих деформациях бывает много меньше единицы. Поэтому Δξ , так что слагаемым Δξ в сумме Δx+Δξ, можно пренебречь).
Подставив найденные значения массы, ускорения и силы в уравнение второго закона Ньютона, получим
Наконец, сократив на SΔx, придем к уравнению
которое представляет собой волновое уравнение, написанное для случая, когда ξ не зависит от у и z. Сопоставление уравнений (4.7) и (5.6) дает, что
|
Таким образом, фазовая скорость продольных упругих волн равна корню квадратному из модуля Юнга, деленного на плотность среды. Аналогичные вычисления для поперечных волн приводят к выражению
|
где G – модуль сдвига.
§ 6. Энергия упругой волны
Пусть в некоторой среде распространяется в направлении оси х плоская продольная волна
x = a cos ( wt − kx + a )
Выделим в среде элементарный объем ΔV, настолько малый, чтобы скорость движения и деформацию во всех точках этого объема можно было считать одинаковыми и равными, соответственно, и .
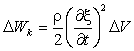Выделенный нами объем обладает кинетической энергией
(ρΔV – масса объема, – его скорость).
Согласно формуле (25.4) 1-го тома рассматриваемый объем обладает также потенциальной энергией упругой деформации
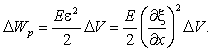
(ε = – относительное удлинение цилиндра, Е — модуль Юнга среды). Заменим в соответствии с (5.7) модуль Юнга через ρυ2 (ρ – плотность среды, υ – фазовая скорость волны). Тогда выражение для потенциальной энергии объема ΔV примет вид
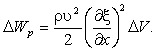
Выражения (6.2) и (6.3) в сумме дают полную энергию
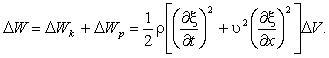
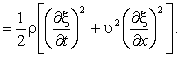Разделив эту энергию на объем ΔV, в котором она содержится, получим плотность энергии
|
Дифференцирование уравнения (6.1) один раз по t, другой раз по x дает
Подставив эти выражения в формулу (6.4) и приняв во внимание, что k2υ2 = ω2, получим
|
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10