Свойства жидкостей
Краевые углы смачивающей (1) и несмачивающей (2) жидкостей.
Наблюдающиеся в этих случаях явления получили общее название капиллярных. Детальная теория капиллярных явлений была разработана в ХIХ веке главным образом в работах английского физика Т.Юнга, французского физика П.Лапласа, немецкого математика К.Гаусса и русских учёных А.Ю. Давыдова и И.С. Громеки.
Капиллярные эффекты, широко известные в технике и быту, в основном обусловлены тем, что благодаря действию сил поверхностного натяжения давление в нутрии жидкости может отличаться на некоторую величину ∆p от внешнего давления p газа или пара над поверхностью жидкости.
Формула Лапласа
Рассмотрим поверхность жидкости, опирающуюся на некоторый плоский контур. Если поверхность жидкости не плоская, то стремление её к сокращению приведёт к возникновению давления, дополнительного к тому, которое испытывает жидкость с плоской поверхностью. В случае выпуклой поверхности это дополнительное давление положительно, в случае вогнутой поверхности – отрицательно. В последнем случае поверхностный слой, стремясь сократиться, растягивает жидкость.
Величина добавочного давления, очевидно, должна возрастать с увеличением коэффициента поверхностного натяжения α и кривизны поверхности. Вычислим добавочное давление для сферической поверхности жидкости. Для этого рассечём сферическую каплю жидкости диаметральной плоскостью на два полушария (рис. 5).
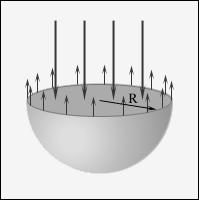
Рис. 5
Сечение сферической капли жидкости.
Из-за поверхностного натяжения оба полушария притягиваются друг к другу с силой, равной:
F=lα=2πRα
Эта сила прижимает друг к другу оба полушария по поверхности S=πR2 и следовательно, обуславливает дополнительное давление:
∆p=F/S=(2πRα)/ πR2=2α/R (4)
Кривизна сферической поверхности всюду одинакова и определяется радиусом сферы R. Очевидно, что чем меньше R, тем больше кривизна сферической поверхности. Кривизну произвольной поверхности принято характеризовать так называемой средней кривизной, которая может оказаться различной для разных точек поверхности.
Средняя кривизна определяется через кривизну нормальных сечений. Нормальным сечением поверхности в некоторой точке называется линия пересечения этой поверхности с плоскостью, проходящей через нормаль к поверхности в рассматриваемой точке. Для сферы любое нормальное сечение представляет собой окружность радиуса R (R-радиус сферы). Величина H=1/R даёт кривизну сферы. В общем случае различные сечения, проведённые через одну и ту же точку, имеют различную кривизну. В геометрии доказывается, что полусумма обратных радиусов кривизны
H=0,5(1/R1+1/R2) (5)
для любой пары взаимно перпендикулярных нормальных сечений имеет одно и тоже значение. Эта величина и есть средняя кривизна поверхности в данной точке.
Радиусы R1 и R2 в формуле (5) – алгебраические величины. Если центр кривизны нормального сечения находиться под данной поверхностью, соответствующий радиус кривизны положителен, если центр кривизны лежит над поверхностью, радиус кривизны отрицателен.
Для сферы R1=R2=R, так что в соответствии с (5) H=1/R. Заменив в (4) 1/R через H, получим, что
∆p=2Hα (6)
Лаплас доказал, что формула (6) справедлива для поверхности любой формы, если под H понимать среднюю кривизну поверхности в это точке, под которой определяется дополнительное давление. Подставив в (6) выражение (5) для средней кривизны, получим формулу для добавочного давления под произвольной поверхностью:
∆p=α(1/R1+1/R2) (7)
Она называется формулой Лапласа.
Добавочное давление (7) обуславливает изменение уровня жидкости в капилляре, вследствие чего называется иногда капиллярным давлением.
Существование краевого угла приводит к тому, что вблизи стенок сосуда наблюдается искривление поверхности жидкости. В капилляре или в узком зазоре между двумя стенками искривленной оказывается вся поверхность. Если жидкость смачивает стенки, поверхность имеет вогнутую форму, если не смачивает – выпуклую (рис . 4). Такого рода изогнутые поверхности жидкости называются менисками.
Если капилляр погрузить одним концом в жидкость, налитую в широкий сосуд, то под искривлённой поверхностью в капилляре давление будет отличаться от давления по плоской поверхностью в широком сосуде на величину ∆p, определённую формулой (7). В результате при смачивании капилляра уровень жидкости в нём будет выше, чем в сосуде, при несмачивании – ниже.
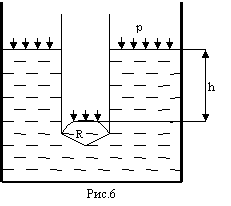Рассмотрим для примера случай круглого капилляра радиуса r, погружённого в большой сосуд с жидкостью, несмачивающей стенки капилляра. При этом внутри капилляра образуется мениск, и под действием дополнительного давления ∆p жидкость в капилляре опускается на некоторую глубину, как это показано на рис.6. В широком сосуде благодаря действию силы тяжести можно считать поверхность жидкости практически плоской. В узкой трубке, напротив, можно пренебречь действием сил тяжести по сравнению с силами поверхностного натяжения и поверхность жидкости считать сферой некоторого радиуса R. Из рисунка 6 видно, что R=r/|cosθ|, где θ – краевой угол на границе жидкость - твёрдая стенка.
На уровне поверхности в капилляре давление жидкости равно p+∆p=p+2α/R, где p – внешнее давление в газе. По закону сообщающихся сосудов оно должно быть равно полному давлению на этом уровне в широком сосуде p+ρgh, где ρgh – гидростатическое давление столба жидкости плотности ρ на глубине h (g – ускорение силы тяжести). Приравнивая, получим:
p+2α/R= p+ρgh (8), откуда
h=2α/ρgR=2α|cosθ|. (9)
В точности такое же выражение мы получим и для высоты поднятия жидкости, смачивающей стенки капилляра радиуса r. При полном смачивании (например вода –стекло) θ=0, cosθ=1, радиус мениска R равен радиусу капилляра r и высота поднятия жидкости равна