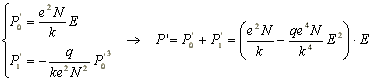Появление мощных источников когерентного светового излучения
Содержание.
Введение.
1. Поляризация диэлектрика в постоянном электрическом поле
2. Поляризация диэлектрика в световом поле
3. Нелинейное взаимодействие электромагнитных волн
4. Генерация второй гармоники (ГВГ)
5. Фазовый синхронизм при генерации второй гармоники
6. Вынужденное комбинационное рассеяние (ВКР)
7. Макроскопическая теория ВКР. Стоксово рассеяние.
8. Антистоксово рассеяние
9. Самофокусировка света
Введение.
Появление мощных источников когерентного светового излучения (лазеров) привело к возникновению нового направления исследований, связанного с изучением взаимодействия мощных когерентных потоков электромагнитного излучения с веществом, получившего название "Нелинейная оптика".
Оптические эффекты, характер которых зависит от интенсивности излучения, называют нелинейными, а область оптики, изучающая нелинейные оптические эффекты (оптика мощных световых потоков) - нелинейной оптикой.
До появления лазеров число нелинейных оптических эффектов можно было перечислить по пальцам. Существовавшие до лазеров источники давали световые волны слишком малой интенсивности и, как следствие, этого большинство наблюдаемых оптических эффектов не зависело от интенсивностей волн. Только после появления лазеров - источников света, позволяющих получить световые волны с напряженностями полей 107 . 109 В/см и выше, т.е. поля, сравнимые с внутриатомными - нелинейные явления в оптике стали предметом пристального изучения.
Поляризация диэлектрика в постоянном электрическом поле
Любой электромагнитный процесс в среде описывается уравнениями Максвелла:
|
|
(1) |
где E(r,t), H(r,t) - вектора напряженностей электрического и магнитного полей в точке r в момент t; r - плотность зарядов; j - плотность тока; D и B - вектора электрической и магнитной индукции.
Однако этих уравнений недостаточно для решения электромагнитной задачи, необходимы материальные уравнения, устанавливающие дополнительные связи между указанными векторами.
|
D=e0E+P', B=m0H+M', j=sE |
(2) |
Уравнения (2) устанавливают связь между вектором макроскопической поляризации среды P', вектором макроскопической намагниченности среды M' и векторами D и B, а также между плотностью тока j и напряженностью электрического поля E. Далее не будем учитывать магнитные свойства среды.
В изотропном случае макроскопическая поляризация среды зависит от напряженности электрического поля E. Коэффициентом пропорциональности в такой зависимости является диэлектрическая восприимчивость среды c(E), которая в общем случае тоже зависит от E. Если учесть эту зависимость, то для уравнения (2) получим:
|
P'=e0 c(E) E ® (2) : D=(1+c(E)) e0 E = e(E) E |
(3) |
Величина e(E)=1+c(E) называется диэлектрической проницаемостью.
В слабых полях восприимчивость среды (и диэл. проницаемость) - константа, не зависящая от напряженности электрического поля. Следовательно, реакция среды на внешнее поле - линейная:
|
P'=e0 c0 E, D=(1+c0) e0 E = e0 e E, e=1+c0 |
(3a) |
Нелинейные эффекты проявляются лишь тогда, когда поля достаточно сильны и величины c и e уже нельзя считать не зависимыми от напряженности поля. Чтобы проиллюстрировать появление нелинейной зависимости величин c и e, вычислим их в рамках простой классической задачи. Рассмотрим газ, состоящий из атомов (два точечных заряда: ядро и электрон) без постоянного электрического дипольного момента. В отсутствие внешнего поля положение точечных зарядов совпадает. Поместим его в постоянное электрическое поле. Заряды в каждом атоме сместятся на некоторое расстояние. Для простоты будем считать, что смещение электрона совпадает с направлением внешнего электрического поля. Тогда можно не учитывать векторного характера величин, входящих в задачу, и оперировать скалярами. Таким образом, атомы приобретут дипольный момент d = e r.
Если было N атомов, то макроскопическая поляризация
|
P' = N d = N e r |
(4) |
На электрон действуют две силы: одна - действие электрического поля - FE = e E, а вторая - упругая - возвращает электрон в прежнее положение FУ = - k r - q r3 (эта сила в общем случае нелинейно зависит от смещения электрона). Приравняем их и получим уравнение для определения смещения электрона во внешнем поле.
|
e E = k r + q r3; |
(5) |
Из (4) выражаем r и подставляем в (5) и получаем нелинейное уравнение для поляризации:
|
|
(6) |
Решим его относительно P', считая член с P' 3 малым. Пусть P' = P'0 + P'1 (два порядка малости), тогда, подставив их в (6), получим два уравнения (одно для членов нулевого порядка малости, другое - для членов первого порядка малости) и решим их.
|
|
(7) |
Перейти на страницу: 1 2 3 4 5 6 7 8