Методы расчета электрических полей (конспект лекций)
.
Поскольку в любой точке поверхности проводника 
должно выполняться условие равенства потенциала его поверхности приложенному напряжению, то получаем следующее интегральное уравнение относительно неизвестного распределения заряда s по поверхности 
:
. (3.1)
После того, как из уравнения (3.1) определяется распределение s, можно рассчитать параметры поля в любой точке пространства.
Интегральные методы расчета электростатических полей разделяют по способу размещения фиктивной поверхности внутри поверхности :
1. Поверхность целиком располагается внутри поверхности , нигде не пересекаясь с последней. Соответствующий метод называется методом эквивалентных зарядов (МЭЗ). Чтобы упростить его реализацию, в большинстве случаев распределение заряда по поверхности полагается не непрерывным, а дискретным. Это означает, что на поверхности размещаются точечные, линейные, кольцевые или какие-либо иные сосредоточенные эквивалентные заряды (ЭЗ). Выбор их конкретного вида определяется формой тела.
2. Поверхность целиком совпадает с поверхностью . Соответствующий метод называется методом интегральных уравнений (МИУ). Таким образом, в МИУ заряд полагается распределенным по поверхности тела .
Ниже методы эквивалентных зарядов и интегральных уравнений будут рассмотрены более подробно.
3.2. Метод эквивалентных зарядов
Как было сказано выше, метод эквивалентных зарядов основан на замещении реального непрерывного распределения заряда по поверхности проводящих и диэлектрических тел совокупностью дискретных эквивалентных зарядов, расположенных внутри тел. Значения ЭЗ определяются из условия эквипотенциальности поверхностей проводников (1.10) , а также из условий неразрывности тангенциальной составляющей вектора напряженности электрического поля (1.3) и нормальной составляющей вектора электрического смещения (1.4) на границах раздела диэлектриков.
Начнем изучение метода эквивалентных зарядов с простейшего случая, когда полеобразующая система не содержит диэлектрических тел.
3.2.1. Расчет электростатического поля проводников.
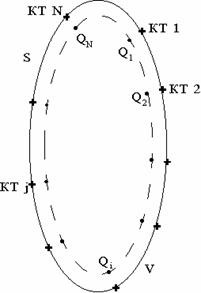
Рассмотрим проводник, ограниченный поверхностью , к которому приложено напряжение V (рис. 3.2).
В данном случае реальное распределение заряда по поверхности тела замещается системой N точечных эквивалентных зарядов 
, расположенных внутри тела. На поверхности размещается N контурных точек (КТ) 
. Потенциал каждой контурной точки 
должен быть равен приложенному напряжению 
. Тогда для каждой КТ можно записать следующее уравнение:
, (3.2)
где 
– расстояние от i-го заряда до j-ой контурной точки, 
. Таким образом, мы имеем систему из N линейных алгебраических уравнений с N неизвестными .
|
Рис. 3.2. К расчету электростатического поля методомэквивалентных зарядов. |
Система уравнений (3.2) может также быть записана в матричной форме
, (3.3)
где P – матрица потенциальных коэффициентов размерности 
; Q – вектор-столбец ЭЗ 
; V – вектор-столбец потенциалов КТ 
. Элементы 
матрицы потенциальных коэффициентов P определяются по формуле
.
Система линейных алгебраических уравнений (3.3) может быть решена относительно неизвестных значений ЭЗ, например, методом Гаусса. После этого составляющие 
вектора напряженности электрического поля 
в любой точке пространства с координатами 
определяются следующим образом:
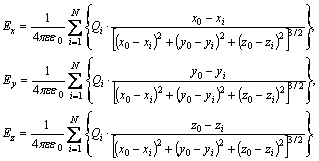(3.4)
Здесь 
- координаты эквивалентных зарядов .
Полный заряд проводника, ограниченного поверхностью определяется как
Перейти на страницу: 1 2 3 4 5