Рефераты по Физике

Энтропия. Теория информации

Страница 11

е е е е е .

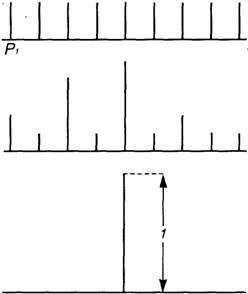
Этот случай соответствует жесткой детерминации (незатухающий строго периодический процесс).

Соответствующее жесткой детерминации распределение вероятностей, при котором некая вероятность Рк равна 1, а все остальные - равны 0, в общем виде запишется как

Рк=1 (3.9)

Р1 = Р2 = . . .= Рк-1 = Рк+1=. . .= 0 (3.10)

а)

Р1 Р2

Pn

б)

в)

Равномерное распределение вероятностей

Нr = Hmax

Дифференцировка вероятностей при соблюдении условия

i=N

S pi = 1

i=1

Hmax > Hr > 0

Предельный случай дифференцировки вероятностей

Нr =0

Рис. 1

При подстановке этих значений в функцию энтропии :

Hr =

i = N

pi log pi

(3.11)

S

i = 1

получаем :

Hr=0 (3.12)

Подставляя (3.9) в (3.4), получаем :

D IS = Hmax (3.13)

Hr = 0

D IS = Hmax

Hr = Hmax

D IS = 0

Все стадии перехода от состояния максимальной энтропии, описываемого условиями (3.4), (3.5), (3.6), к состоянию жесткой детерминации, которому соответствуют условия ( 3.9 ) + (3.13) можно представить в виде дуги, соединяющей исходное состояние Н с конечным состоянием К (рис. 2).

Рис. 2

На рис.3 изображена расширяющаяяся иерархическая спи­раль, которая может служить моделью формирования иерархических упорядоченных структур.

Пусть нижний уровень этой спирали (п = 0) соответствует на­чальному алфавиту, состоящему из N0 различных элементов (букв, атомов, нуклеотидов и др.).

n = 3

n = 2

n = 1

n = 0

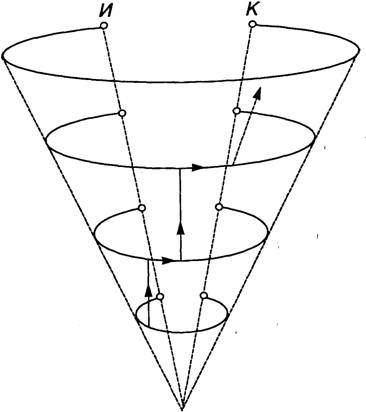
рис. 3

Тогда на уровне N = 1 из этого алфавита можно составить N1 «слов». Если каждое слово состоит из K1 букв, то из N0 букв можно составить число слов, равное:

N1 = N0K1 (3.14)

Соответственно, на уровне п = 2 из N1 «слов» можно соста­вить количество «фраз», равное:

N2=N1K2=N0K1K2 (3.15)

где Кг - число входящих в каждую «фразу» «слов»

Для упрощения математических выражений мы уже приняли одно допущение, сказав, что все слова содержат одинаковое ко­личество букв (К1), а все фразы содержат одинаковое количество слов (К2). Очевидно, что в реальных системах (например, в письменных текстах ) эти условия не соблюдаются. Однако для выполнения общих свойств нашей информационно -энтропийной модели подобные упрощения вполне допустимы, поэтому мы введем еще одно допущение:

K1 = К2 = К (3.16)

Подставив (3.16) в (3.15), мы получим :

N2=N0K2 (3.17)

Проводя аналогичные операции для любой (п-ой) ступени при условии:

K1 = K2 = … = Кп = К,

получим:

Nn = N0K2 (3.18)

Рассмотрим пример, иллюстрирующий увеличение разнообразия (числа различимых элементов) с переходом на более высокие уровни изображенной на рис . 3.3 спирали в соответствии с форму­лами (3.14) + (3.18).

Перейти на страницу:  1  2  3  4  5  6  7  8  9  10  11  12  13  14