Теория припекания порошковых слоев в двухпараметрическрй модели вязко пористой среды
§ 1. Двухпараметрическая модель припекаемой системы.
Рассмотрим одну из возможных моделей припекаемой системы, в которой с течением времени происходит перестройка, сопровождающаяся понижением активности. Эта модель для случая жидкофазных прослоек была предложена в работе [4], а в более общем случае рассматривалась в [8].
Предположим, что система в каждый момент времени припекания представляет из себя «раствор» двух подсистем различной активности, которые характеризуются кинетическими константами 
и 
в зависимости
(1)
Обозначая через 
объем компактного вещества подсистемы I и соответственно, через 
объем компактного металла подсистемы II, положим:
(2)
Это неравенство, вообще говоря, может быть не очень сильным.
Введем объемные доли подсистем в «растворе»
; 
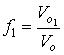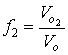
и (3)
Компактное вещество подсистем II, I будем принимать в нашей модели несжимаемым. Предполагается, что изменение объема более активной подсистемы I с течением времени происходит согласно простейшему уравнению:
(4)
Отсюда следует, что
(5)
Здесь 
- начальная объемная доля подсистемы I в «растворе».
Таким образом, получим для объемных долей подсистемы соотношения:
; 
(6)
Введено характерное время существования (время жизни) подсистемы I
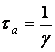(7)
В простейшем случае можно предположить, что и тогда
; 
(8)
Дальнейшие рассуждения связаны с рассмотрением диссипативной функции «раствора», которую, очевидно, можно представить в виде суперпозиции диссипативных функций подсистем.
(9)
Используя следующие приближение:
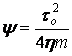, (10)
будем иметь:
(11)
Приняли касательное напряжение в «растворе» одинаковым для всех подсистем.
Переходя к усредненным по объему всей системы параметрам, находим:
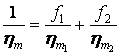(12)
Если положить 
, то для кинетической константы «раствора» будем иметь уравнение:
(13)
в случае 
(14)
Проинтегрируем правую часть
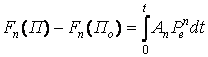
с учетом уравнения (13) и соотношений (8).
Получим:
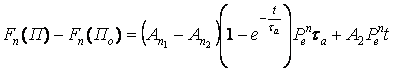(15)
Из общего уравнения (15) имеем приближенные уравнения для начальной и конечной стадии процесса:
(16)
(17)
Проанализируем влияние скорости нагрева на процесс припекания, используя результаты работы [10].
Положим скорость нагрева
(18)
и примем кинетическую константу в виде:
(19)
где упрощено представлена энергия активизации высокотемпературной ползучести в виде:
(20)
Интегрируя кинетическое уравнение, сделав замену переменной, согласно
(21)
получим:
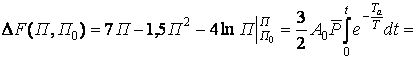
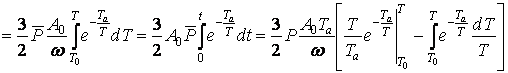(22)
Учитывая определение
,
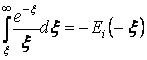и выполняя в (22) замену переменной, находим:
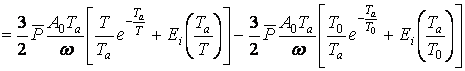(23)
Для области 
можно воспользоваться приближенным представлением [2, 3]:
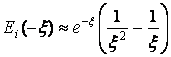(24)
Получится следующее уравнение процесса припекания слоя:
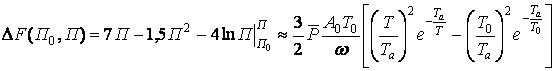(25)
Поскольку 
, второе слагаемое в скобках справа можно опустить.
Тогда уравнение упростится:
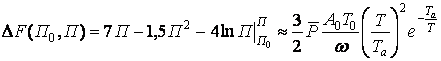(26)
Из анализа (26) следует, что для получения заданной пористости покрытия необходимо согласовывать величину среднего активирующего давления со скоростью нагрева, и более высокие значения требуют больших, активирующих процесс припекания, давлений.
Величину активирующего давления следует ограничивать значениями 30-40 Мпа. Нагрев необходимо проводить с уменьшенной скоростью.
Перейти на страницу: 1 2 3 4 5 6