Рефераты по Физике

Моделирование в физике элементарных частиц

Страница 13

$V^D = - (D \cdot E) = - D(\sigma \cdot E)$ Прямое магнитодипольное взаимодействие нейтрона с магнитным полем вызывает прецессию вектора спина частицы вокруг вектора H., направляя электрическое поле, например, по магнитному полю или против него, мы уменьшим или увеличим угловую скорость прецессии $\omega^{\pm} = (\mu \cdot H \pm D \cdot E)/ \hbar $, Изменение угла $\Delta \varphi = (\omega^{+} - \omega^{-}) \tau = 2(D \cdot E) \tau / \hbar$при переключении знака электрического поля непосредственно содержит информацию об ЭДМ и подлежит экспериментальному определению в методе УХН - магниторезонансном методе с использованием ультрахолодных нейтронов. Последние обладают столь низкой кинетической энергией, что полностью отражаются от стенок ловушки, не имея возможности преодолеть потенциальный барьер и проникнуть внутрь вещества. В результате их можно накапливать и хранить в полости. Идея о возможности хранения ультрахолодных нейтронов в замкнутой полости за счет полного внешнего отражения принадлежит Я.Б. Зельдовичу.

Очевидно, что эффекты, которые обусловлены наличием у нейтрона ЭДМ, должны расти с возрастанием электрического поля, приложенного к нейтрону, а также с увеличением времени пребывания нейтрона в этом поле. Абсолютная погрешность при измерениях ЭДМ указанным способом, характеризующая чувствительность метода, оценивается как

$\delta (D) = \hbar / (E \tau \sqrt{N})$

Величина $E \tau$обусловливает экспериментально наблюдаемый эффект, например изменение скорости счета нейтронов в детекторе при изменении направления электрического поля или спина нейтрона. N - полное число зарегистрированных детектором событий за все время измерения. Таким образом, чтобы улучшить чувствительность метода, нужно увеличивать электрическое поле, действующее на нейтрон, время пребывания нейтрона в этом поле, а также стараться собрать в области действия поля как можно больше самих нейтронов.

Существование в веществе сильных межатомных электрических полей $\sim 10^8-10^9$В/см следует из простых соображений: энергия выхода электронов из вещества лежит в интервале 1-10 эВ, значит, разность потенциалов на атомах и между ними 1-10 В; межатомные же расстояния около $10^{-8}$см. Эти поля быстро осциллируют в веществе и поэтому при движении частиц обычно усредняются, обращаясь в нуль.

Однако бывают ситуации, например при дифракции нейтронов в монокристаллах, когда, в силу регулярности потенциала кристалла и соответствующей регулярности волновой функции нейтрона в нем, нейтрон может оказаться в сильном электрическом поле на протяжении всего времени прохождения кристалла. Именно это обстоятельство, т.е. эффективное взаимодействие с внутрикристаллическим полем нейтронов при их динамической дифракции по Лауэ в прозрачном нецентросимметричном кристалле, и было использовано при постановке нового - дифракционного - опыта по уточнению верхнего предела на величину ЭДМ нейтрона.

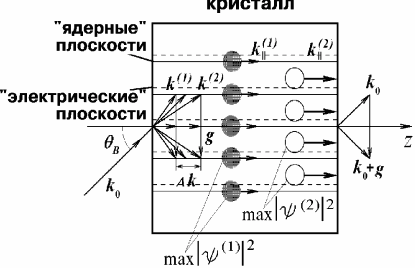
Физика явлений, лежащих в основе метода, следующая. Из динамической теории дифракции следует, что движение нейтрона в кристалле в направлениях, близких к брэгговским, можно описать волнами двух типов $\Psi^{(1)}$и $\Psi^{(2)}$. Это две волны, сформированные в результате многократного отражения нейтрона от кристаллографических плоскостей, причем стоячие в перпендикулярном к плоскостям направлении. Дифрагирующие нейтроны в этих состояниях, распространяясь в среднем вдоль плоскостей, оказываются сконцентрированными на "ядерных" плоскостях и между ними соответственно.

В нецентральносимметричных кристаллах для некоторых систем кристаллографических плоскостей положения максимумов электрического потенциала смещены относительно максимумов ядерного потенциала:

$V^{N}(r) = 2V^{N}_{g} \cos(gr)$, $V^{E}(r) = 2V^{E}_g \cos(gr + \phi_g)$.

Здесь $V^{N}(r)$- ядерный потенциал, ответственный за дифракцию нейтронов, $V^{E}(r)$- электрический, g - вектор обратной решетки, характеризующий выбранную систему плоскостей; $2V_{g}^{N}$, $2V_{g}^{E}$- амплитуды ядерного и электрического потенциалов соответственно. Величина $\phi_g$характеризует смещение максимумов ядерного потенциала относительно максимумов электрического. В результате нейтроны в состояниях $\Psi^{(1)}$и $\Psi^{(2)}$оказываются в сильных ($\sim 10^8$ В/см) межплоскостных электрических полях противоположного знака:

$E_g = \pm gV_{g}^{E} \sin {\phi_g}$.

Наличия таких внутрикристаллических полей еще недостаточно для повышения точности измерения ЭДМ. Важное свойство приведенное на схеме дифракции по Лауэ - возможность увеличить время пребывания нейтрона в электрическом поле кристалла путем перехода к углам Брэгга $\theta_B$, близким к $\pi/2$. Причина в том, что при дифракции по Лауэ нейтрон, имея полную скорость v, вдоль кристаллографических плоскостей в среднем движется со скоростью $v \Vert = v \cos \theta_B$, которая может быть существенно уменьшена по сравнению с v при выборе угла дифракции $\theta_B$вблизи $\pi/2$. Поскольку при этом $\cos \theta_B \approx \pi /2 - \theta_B$, время $\tau = L/v_{\|} \sim (\pi/2 - \theta_B)^{-1}$растет по мере приближения $\theta_B$к $\pi/2$. Максимально близкий к $\pi/2$угол Брэгга определит максимальную чувствительность метода. Дальнейшее его увеличение, в принципе может оказаться невозможным.

Рис 7

Движение нейтронов вдоль кристаллографических плоскостей при дифракции. Кружками изображены области максимальной концентрации нейтронов в состояниях $\Psi^{(1)}$и $\Psi^{(2)}$, здесь частицы двигаются в электрических полях разного знака. k - волновые векторы нейтрона, связанные с его скоростью k=mv/h; так как нейтроны в состояниях $\Psi^{(1)}$и $\Psi^{(2)}$оказываются в разных потенциалах, их кинетические энергии, а значит, и k, отличаются. На выходе из кристалла показаны волновые векторы двух продифрагировавших пучков, прямого и отраженного. Их геометрическое расположение определяет условие наблюдения брэгговских пиков дифракции, задающее угол Брэгга.

Перейти на страницу:  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19