Система уравнений Максвелла в сплошной среде. Граничные условия
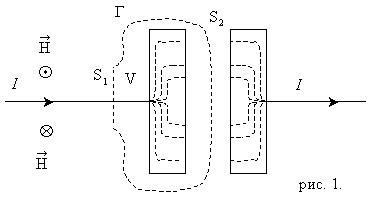
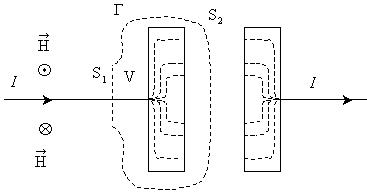Этот ток непостоянен во времени (в момент, когда напряжение на конденсаторе становится равным U, ток прекращается). Линии тока проводимости терпят разрыв в промежутке между обкладками конденсатора.
Возьмём круговой контур Г, охватывающий провод, по которому течёт ток к конденсатору, и проинтегрируем соотношение (3.1) по пересекающеё провод поверхности S1, ограниченной контуром:
.
Преобразовав левую часть по теореме Стокса, получим циркуляцию вектора 
по контуру Г:
(3.3)
(I – сила тока заряжающего конденсатор). Проделав такие же вычисления для поверхности S2, придём к явно неверному соотношению:
(3.4)
Полученный результат указывает на то, что в случае изменяющихся со временем полей уравнение (3.1) перестаёт быть справедливым. Напрашивается вывод, что в этом уравнении отсутствует слагаемое, зависящее от произвольных полей во времени. Для стационарных полей это слагаемое обращается в нуль.
На неправомерность уравнения (3.1) в случае нестационарных полей указывает также, следующие соображения. Возьмём дивергенцию от обеих частей соотношения (3.1):
Дивергенция ротора должна быть обязательно равна нулю. Таки образом, можно прийти к выводу, что дивергенция вектора 
также должна быть всегда равной нулю. Однако этот вывод
противоречит уравнению непрерывности, где отлична от нуля.
Чтобы согласовать уравнения (3.1) и (3.2), Максвелл ввел в правую часть уравнения (3.1) дополнительное слагаемое. Естественно, что это слагаемое должно иметь размерность плотности тока. Максвелл назвал его плотностью тока смещения. Таким образом, согласно Максвеллу уравнение (3.1) должно иметь вид:
(3.5)
Сумму тока проводимости и тока смещения принято называть полным током. Плотность полного тока равна:
(3.6)
Если положить дивергенцию тока смещения равной дивергенции тока проводимости, взятой с обратным знаком,
(3.7)
то дивергенция правой части уравнения (3.5), так же как и дивергенция левой части, всегда будет равна нулю.
Заменив в (3.7) 
согласно (3.2) через 
, получим следующее выражение для дивергенции тока смещения:
. (3.8)
Чтобы связать ток смещения с величинами, характеризующими изменение электрического поля со временем, воспользуемся соотношением:
Продифференцировав это соотношение по времени, получим:
Теперь поменяем в левой части порядок дифференцирования по времени и по координа -там. В результате придём к следующему выражения для производной 
по 
.
.
Подстановка этого выражения в формулу (3.8) даёт:
.
Отсюда
(3.9)
Подставив выражение (3.9) в формулу (3.6), придём к уравнению
.
Каждое из векторных уравнений (1) и (3) эквивалентно трем скалярным уравнениям, связывающим компоненты векторов, стоящих в левой и правой частях равенств. Воспользовавшись правилом раскрытия дифференциальных операторов, можно записать их в следующем виде:
; 
; 
(5)
(6)
для первой пары уравнений, и:
; 
; 
(7)
(8)
для второй.
Всего получилось 8 уравнений, в которых входят 12 функций (по три компоненты векторов 
, 
, 
, .) Поскольку число уравнений меньше числа известных функций, уравнений (1) - (4) недостаточно для нахождения полей по заданным распределениям зарядов и токов. Чтобы осуществить расчёт полей, нужно дополнить уравнения Максвелла уравнениями, связывающими и с , а также с . Эти уравнения имеют вид.
Перейти на страницу: 1 2 3 4 5 6 7 8