Оптимизация профиля отражения частотных фильтров излучения с использованием модулированных сверхрешеток
На самом деле здесь возможно два варианта (рисунок № 4 и рисунок № 5, график № 25 и графики № 26 и № 27). Для порядка вкратце рассмотрим оба. Первый из них (рисунок № 4 и график № 25) назовем псевдогауссовым, ввиду того, что параметр (в нашем случае – оптический путь) сначала уменьшается, а потом увеличивается, то есть функционально изменяется обратно функции Гаусса.
Схематически псевдогауссову модуляцию можно изобразить следующим образом:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 2.2 2.2 2.2 2.2 2.2 2.2 2.2
2.2 2.2 2.2 2.2 2.2 2.2 2.2
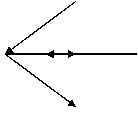 |
1.44 1.44 1.44 1.44 1.44 1.44 1.44
Рисунок 4. Схематичное представление структура с псевдогауссовой
модуляцией.
То есть происходит одновременное утолщение и утоньшение слоев с разными показателями преломления.
Оптический путь такой структуры схематично представлен на графике № 25.
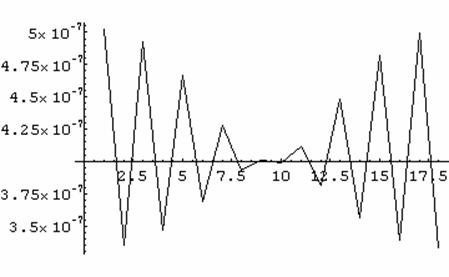
График 25. Схематичное изображение оптического пути для
псевдогауссовой модуляции структуры.
Второй вариант – сначала утолщение, а потом утоньшение (но обязательно одновременное для слоев с разными показателями преломления) по функции Гаусса, как это показано на рисунке 5.

 2.2 2.2 2.2 2.2 2.2 2.2 2.2
2.2 2.2 2.2 2.2 2.2 2.2 2.2
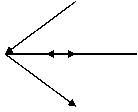 |
1.44 1.44 1.44 1.44 1.44 1.44 1.44
Рисунок 5. Схематичное представление структура с гауссовой
модуляцией.
Оптический путь при такой модуляции схематично показан на графике № 26 и графике № 27.
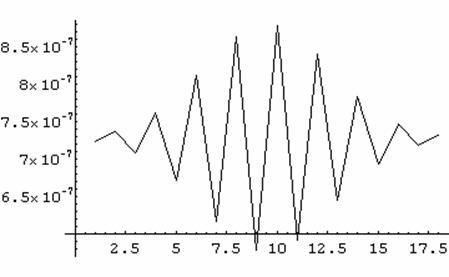
График 26. Схематичное изображение оптического пути для
гауссовой модуляции структуры (малое число слоев (18)).
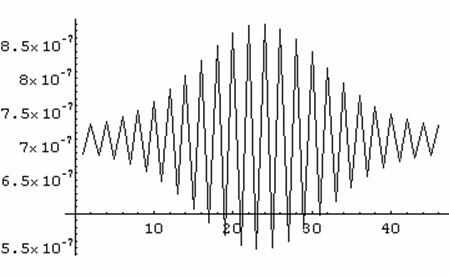
График 27. Схематичное изображение оптического пути для
гауссовой модуляции структуры (большое число слоев (46)).
При псевдогауссовой модуляции появляется довольно беспорядочный набор узких пиков, чередующихся с сильно возмущенными зонами, с коэффициентом отражения от 0.2 до 0.7. И вся эта картинка «плавает» и диспергирует в зависимости от угла падения излучения. Приводить ее здесь не будем. Сейчас перейдем непосредственно к бинарным структурам, промодулированным с помощью функции Гаусса exp(-x2/s2), где параметр s = L/4. Здесь L – ширина всей структуры.
Поскольку все схематические изображения в данном случае выглядят так же, как на графиках № 26 и 27 только с разным числом слоев, не будем приводить их в дальнейшем.
Восьмислойная структура дает следующие результаты:
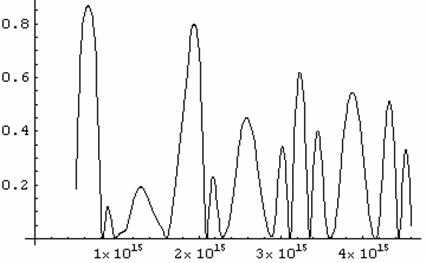
График 28. Зависимости отражения волны для
структуры из восьми слоев при угле падения 00 от частоты.
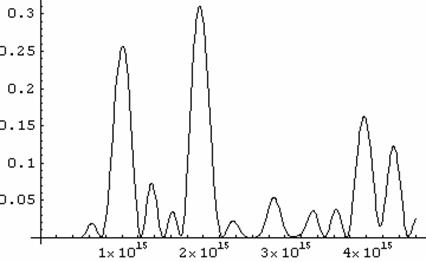
График 29. Зависимости отражения волны для
структуры из восьми слоев при угле падения 450 от частоты.
Получается довольно интересная картина. Четко вырисовывается пик на нужной частоте: 2*1015 – 2.5*1015 Гц. При этом подавляется отражение на смежных частотах. Подводит только малый коэффициент отражения. 0.8 для 00 падения и совсем малый 0.3 при 450 падения луча. Попробуем увеличить их за счет увеличения числа слоев.
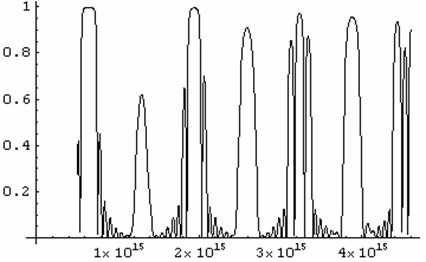
График 30. Зависимости отражения волны для структуры
из восемнадцати слоев при угле падения 00 от частоты.
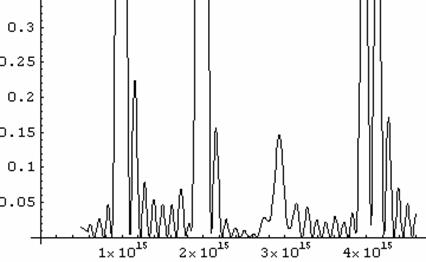
График 31. Зависимости отражения волны для структуры
из восемнадцати слоев при угле падения 450 от частоты.
Результат существенно улучшился. Но теперь ухудшилось пропускание на соседних частотах. Появляется бахрома с разбросом коэффициента отражения до 0.15.
Чтобы уловить общую тенденцию этого направления оптимизации посмотрим еще несколько графиков, постепенно увеличивая число слоев в решетке.
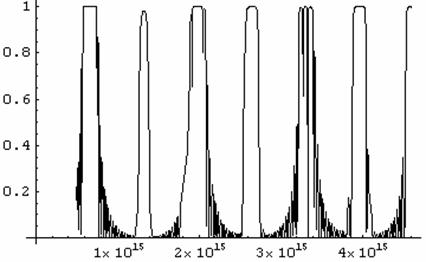
График 32. Зависимости отражения волны для структуры
из тридцати шести слоев при угле падения 00 от частоты.
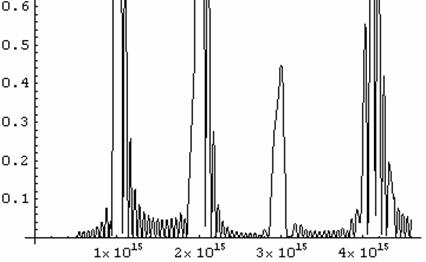
График 33. Зависимости отражения волны для структуры
из тридцати шести слоев при угле падения 450 от частоты.
Теперь бахрома в области пропускания стала чаще. Посмотрим, что дальше будет.
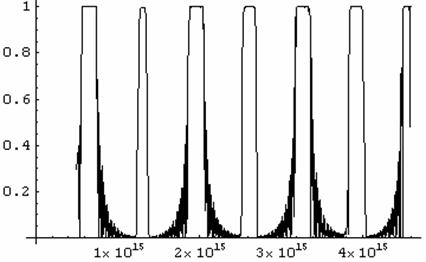
График 34. Зависимости отражения волны для структуры
Перейти на страницу: 1 2 3 4 5 6 7
