Некоторые парадоксы теории относительности
Если выбраны две системы отсчета 
и 
, каждая из которых подобным образом изображает одно и то же пространство-время, то, как это установлено в теории относительности, координаты в системах и связаны так, что интервал 
, определяемый для двух разобщенных событий как
(a)
остается одинаковым при переходе от Е к Е’, т.е.
(b)
Иначе говоря, 
является инвариантом преобразований Лоренца, связывающих координаты и время в и : 
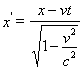, (c)
Из (c), так же как из (a) и (b), следует относительность одновременности пространственно разобщенных событий, т.е. для двух событий, 
в системедвижущейся со скоростью 
, будем иметь 
(d)
В этих свойствах пространственно-временных координат и отражается существо новых представлений о пространстве и времени, связанных в единое геометрического типа многообразие, многообразие с особой, определяемой (а) и (b) четырехмерной псевдоевклидовой геометрией, геометрией, в которой время тесно связано с пространством и не может рассматриваться независимо от последнего, как это видно из (d).
Из этих же представлений вытекают важнейшие следствия для законов природы, выражаемые в требовании ковариантности (т.е. неизменяемости формы) любых физических процессов по отношению к преобразованиям четырехмерных пространственно-временных координат. В требовании также отражается представление о пространстве-времени как о едином четырехмерном многообразии. Так представляют себе физики, конкретно применяющие теорию относительности, ее реальное содержание. При этом понятие относительности приобретает лишь смысл возможной множественности пространственно-временных изображений явлений при абсолютности содержания, т.е. законов природы.
Постулаты Эйнштейна.
Преобразования Лоренца, отражающие свойства пространства-времени, были выведены Эйнштейном, исходя из 2 постулатов: принципа относительности и принципа постоянства скорости света.
1. Законы, по которым изменяются состояния физических систем, не зависят от того, к которой из двух координатных систем, находящихся относительно друг друга в равномерном поступательном движении, эти изменения состояния относятся.
2. Каждый луч света движется в “покоящейся” системе координат с определенной скоростью 
, независимо от того, испускается ли этот луч света покоящимся или движущимся телом.
Значение этих постулатов для дальнейшего развития теории пространства-времени состояло в том, что их принятие прежде всего означало отказ от старых представлений о пространстве и времени, как о многообразиях, не связанных органически друг с другом.
Принцип относительности сам по себе не представлял чего-либо абсолютно нового, т.к. он содержался и в Ньютоновской физике, построенной на базе классической механики. Принцип постоянства скорости света также не был чем-то абсолютно неприемлемым с точки зрения ньютоновских представлений о пространстве и времени.
Однако эти два принципа, взятые вместе привели к противоречию с конкретными представлениями о пространстве и времени, связанные с механикой Ньютона. Это противоречие можно проиллюстрировать следующим парадоксом.
Пусть в системе отсчета в начальный момент 
в точке, совпадающей с началом координат произошла вспышка света. В последующий момент времени 
фронт световой волны, в силу закона постоянства скорости света, распространился до сферы радиуса 
с центром в начале координат системы . Однако в соответствии с постулатами Эйнштейна, это же явление мы можем рассмотреть и точки зрения системы отсчета , движущейся равномерно и прямолинейно вдоль оси 
, так, что ее начало координат и направления всех осей совпадали в момент времени с началом координат и направлениями осей первоначальной системы . В этой движущейся системе, соответственно постулатам Эйнштейна, за время свет также распространится до сферы радиуса
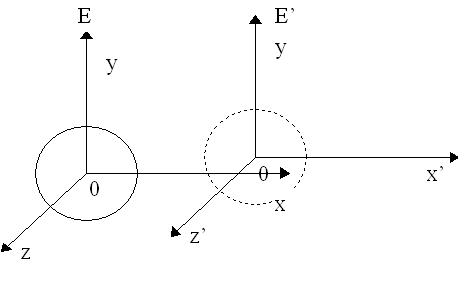
радиуса , однако, в отличие о предыдущей сферы должен лежать в начале координат системы , а не . Несовпадение этих сфер, т.е. одного и того же физического явления, представляется чем-то совершенно парадоксальным и неприемлемым с точки зрения существующих представлений. Кажется, что для разрешения парадокса надо отказаться от принципа относительности, либо от принципа постоянства скорости света. Теория относительности предлагает, однако, совершенно иное разрешение парадокса, состоящее в том, что события, одновременные в одной системе отсчета , неодновременны в другой, движущейся системе , и наоборот. Тогда одновременные события, состоящие в достижении световым фронтом сферы, определяемой уравнением
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10