Концепция современного естествознания
Что произойдет с энергией тела в момент, падения на землю. Тело остановится, следовательно, его кинетическая энергия относительно земли станет равной нулю. Куда денется энергия. Она не исчезнет, а перейдет в так называемую внутреннюю энергию. Внутренней энергией тела называется сумма кинетических и потенциальных энергий всех атомов, из которых состоит тело. Внутренняя энергия обычно определяется параметром системы, который называется температурой. Чем больше температура, тем больше внутренняя энергия и тем больше скорости атомов, составляющих эту систему. Таким образом, при падении тела на поверхность земли а его потенциальная энергия сначала переходит в кинетическую, а затем - во внутреннюю энергию системы тело- земля. Поскольку мерой внутренней энергии системы является температура, потенциальная энергия поднятого тела после его падения пойдет на нагрев самого тела и поверхности земли, Или другими словами, на увеличение кинетической энергии атомов тела и поверхности земли. Отметим, что если рассматривать данное тело как изолированную систему, то его полная энергия, не сохранялась бы. Однако, со включением в систему поверхности земли все встало на свои места. Закон сохранения энергии сработал. https://s-parfum-shop.ru/katalog/akcii купить essens духи со скидкой.
Закон сохранения энергии отражает симметрию явлений природы по отношению к переносу во времени, или, иначе, постоянство законов природы во времени. Проще всего доказать это от противного. Покажем, что если бы законы природы менялись во времени, то энергия не сохранялась бы. Пусть, например, меняется во времени закон всемирного тяготения, и даже не сам закон, а только гравитационная постоянная G (см. формулу 10.7). Поднятое в какой-то момент времени на высоту 
тело будет обладать потенциальной энергией 
, где ускорение свободного падения равно: 
, где М - масса Земли, а Rз - ее радиус. Если гравитационная постоянная G, будет меняться, то вместе с ней будет меняться потенциальная и полная механическая энергия. Налицо нарушение закона сохранения энергии.
Отсюда вывод: если бы законы природы менялись со временем, то это привело бы к нарушению закона сохранения энергии.
Рассмотрим закон сохранения импульса. Импульсом или количеством движения тела называется произведение скорости поступательного движения этого тела на его массу P=mu. Импульсом системы называется векторная сумма импульсов всех тел, образующих эту систему. Если в системе имеются только силы взаимодействия и нет внешних сил, то такая система называется замкнутой. Закон сохранения импульса гласит: полный импульс изолированной системы не меняется, т.е. остается постоянным при любых взаимодействиях внутри этой системы. Отражением какого преобразования пространства или процесса симметрии является этот закон? Он отражает тот факт, что сдвиг начала системы отсчета в произвольном направлении на любое расстояние, не меняет течения явлений природы и никак не отражается на в законах природы. Проще всего это показать следующим образом. Пусть имеется материальная точка массой m, имеющая скоростью u в произвольной системе отсчета К. Импульс материальной точки равен P=mu, где скорость точки u=r’(t). Пусть мы перешли в другую систему отсчета, начало координат которой сдвинуто на постоянный вектор ro относительно системы отсчета К. Как изменится импульс? В системе отсчета K’ он будет равен mu:
.
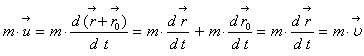Получилось, что импульс тела не меняется при сдвиге начала системы координат на вектор ro, т.е. при переходе от одной системы к другой, неподвижной относительно первой.
Таким образом, закон сохранения импульса является отображением однородности пространства, т.е. отсутствием каких-либо выделенных, «особых» точек в пространстве.
Закон сохранения момента импульса или момента количества движения является отображением еще одного фундаментального свойства пространства - его изотропности.
Момент импульса Lравен векторному произведению радиуса вектора тела на импульс тела: L=[rp]. Т.е. L - это вектор, направленный перпендикулярно векторам r и p и по модулю равный произведению их длин на синус угла a между ними, т.е. L=r×p×sina. Из двух направлений, перпендикулярных векторам r и p, направлениевектора L выбирается по правилу буравчика. При вращение ручки буравчика от r к p в направлении меньшего угла поступательное движение буравчика укажет направление вектора момента импульса. Полный момент импульса системы равен векторной сумме моментов импульса всех тел системы. Система называется замкнутой, если в ней имеются только силы взаимодействия между телами и нет внешних сил. Закон сохранения момента импульса гласит: полный момент импульса тела или изолированной системы не меняется ни при каких взаимодействиях тел внутри этой системы.
Под изотропностью пространства подразумевают отсутствие каких-либо преимущественных или выделенных направлений в пространстве. Все направления в пространстве равноценны и нет ни одного, которое обладало бы каким-то преимуществом перед другими.
Закон сохранения момента импульса и является отображением изотропности пространства. В терминах предыдущего раздела мы можем сформулировать следующее. При применении операции поворота в пространстве момент количества движения тела не меняется, поскольку его величина и направление зависят лишь от длин и взаимной ориентации векторов r и p. Значит, какое бы направление в пространстве мы ни приняли для нашей системы координат, момент импульса тела от этого не изменится. Строгое доказательство этого утверждения требует использование аппарата векторной алгебры и выходит за рамки наших рассмотрений.
Закон сохранения зарядов может быть сформулирован так. Алгебраическая сумма зарядов изолированной системы не меняется ни при каких взаимодействиях внутри этой системы. Понять, отображением каких свойств пространства является этот закон, можно лишь после глубокого знакомства с квантовой механикой. В квантовой механике поведение тела (микрочастицы) описывается волновой функцией - Y, которая в общем случае может быть комплексной. Квадрат модуля этой функции умноженный на элемент объема равен вероятности обнаружить частицу в этом элементе объема. Эта функция тоже может быть подвергнута различным преобразованиям в пространстве и времени. Одно из таких преобразований - записывается как 
, где 
- мнимая единица, 
- некоторое число, 
- заряд. Наглядного физического смысла это преобразование не имеет. Его называют локальным калибровочным преобразованием. Модуль написанного выражения равен единице,
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21