Электрон в потенциальной яме. Туннельный эффект
Содержание
ЭЛЕКТРОН В ПОТЕНЦИАЛЬНОЙ ЯМЕ
РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ
КЛАССИФИКАЦИЯ ТВЕРДЫХ ТЕЛ
ЭЛЕКТРОНЫ И ДЫРКИ
ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ ПРИМЕСЕЙ И ДЕФЕКТОВ
ТУННЕЛЬНЫЙ ЭФФЕКТ
ВВЕДЕНИЕ
ТЕОРИЯ ТУННЕЛЬНОГО ЭФФЕКТА https://persona-spa.ru массаж лингама цены.
ТУННЕЛЬНЫЙ ЭФФЕКТ В ФИЗИКЕ
ТУННЕЛИРОВАНИЕ ЭЛЕКТРОНОВ В ТВЕРДЫХ ТЕЛАХ
КВАНТОВЫЕ ТРАНЗИСТОРЫ
ТУННЕЛЬНЫЙ ДИОД
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
ПРИЛОЖЕНИЕ
Электрон в потенциальной яме
Если ранее мы рассматривали примеры в которых е- мог свободно перемещаться в некоторых областях одномерного пространства. Теперь поместим его в область с низкой потенциальной энергией. Такую область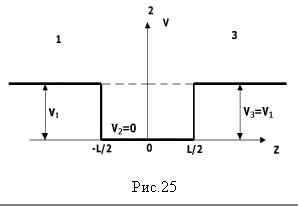 
обычно называют потенциальной ямой.
Профиль потенциальной ямы шириной L показан на рис. 25
Пока Е>V1, решение не отличается от уже известного нам, но когда Е<V1, то положение принципиально изменяется.
Рассмотрение уравнения Шредингера для пространственно однородного потенциала дает следующие результаты.
В области 3 существует только экспоненциально убывающее решение
(п.1)
где 
(п.2)
В области 2 потенциал равен нулю. Здесь возможны решения двух видов - симметричное и антисимметричное (что определяется симметричным распределением потенциала). Соответственно,
(п.3)
(п.4)
Здесь 
(п.5)
В области 1 решение снова должно быть затухающим, но на сей раз в направлении отрицательных Z. Соображениям симметрии удовлетворяет функция
(п.6)
Исследуем сначала симметричное решение. В этом случае надо использовать уравнения (п.1) и (п.3), а так же уравнение (п.6) со знаком "+". В точках Z=L/2 и Z=-L/2 должны выполняться условия непрерывной волновой функции и ее производной. В силу симметрии задачи достаточно удовлетворить граничным условиям в какой-либо одной точке, скажем в точке Z=L/2. Из условия непрерывности волновой функции следует, что
(п.7)
А из условия, налагаемого на производную
(п.8)
Таким образом однородную систему линейных алгебраических уравнений относительно неизвестных коэффициентов A и C. Эта система имеет нетривиальное решение, если ее детерминант равен нулю, т.е.
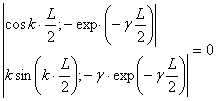
(п.9)
или
(п.10)
Используя (п.2) и (п.5) получим
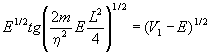
(п.11)
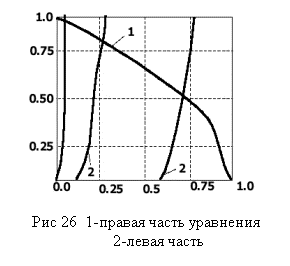
Нелинейное уравнение (п.11) необходимо решить относительно энергии E. Его можно решить на ЭВМ или графически, построив отдельно левую и правую части (п.11). Для примера: m=9.1*10-31кг, ћ=1.05*10-34Дж/Гц, и примем L=10-9м, V1=1.6*10-19Дж
Как видно кривые пересекаются в трех точках, т.е. существуют ровно три решения. Энергия электрона может иметь любое значение в области Е>V1, но если Е<V1, то существуют только три разрешенных энергетических уровня (состояния), (точнее, 3 энергетических уровня для симметричных решений и еще какое-то число для антисимметричных).
Таким образом мы решили задачу, которую с полным основанием можно назвать квантово-механической. Энергия больше не может принимать любое значение. Разрешены только вполне определенные дискретные состояния.
Дискретные энергетические уровни энергии появляются всякий раз, когда мы ограничиваем движение электрона.
Решение приобретает вид дискретного набора волновых функций и уровней энергии.
Итак, для е- в твердом теле уравнение может быть записано в виде:
(1)
Где 
- дифференциальный оператор Лапласа в декартовой системе координат.
Y(x,y,z) - волновая функция E - полная энергия электрона V1(x,y,z) - потенциальная энергия электрона h - постоянная Планка m - масса электрона
Установлено, что уравнение (1) имеет отличные от нуля решения относительно Y(x,y,z) только при некоторых дискретных значениях энергии E. В этих случаях говорят, что имеет место некоторое квантовое состояние. Каждому квантовому состоянию отвечает определенное значение энергии электрона E, а также его импульса mV или ћk.
Для описания квантового состояния используют набор квантовых чисел:
· n (азимутальное квантовое число,
· l (орбитальное квантовое число),
· ml (магнитное орбитальное квантовое число) и
· ms (спиновое число).
Поскольку уравнение (1) имеет отличные от нуля решения только при некоторых дискретных E, то говорят, что электрон занимает некоторые разрешенные энергетические уровни. В соответствии с принципом Паули два электрона в любом атоме не могут находиться в одном и том же квантовом состоянии, число электронов находящихся на одном и том же энергетическом уровне не может превышать числа квантовых состояний.
В твердых кристаллических телах высока концентрация атомов, из-за их близкого расположения между атомами возникает взаимодействие и потенциальная энергия электронов становится периодической функцией пространственных координат.
Перейти на страницу: 1 2 3 4 5