Оптические инструменты, вооружающие глаз
2.4.2. Разрешающая способность глаза.
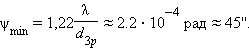 |
Известно, что сетчатка глаза состоит из светочувствительных рецепторов конечного размера. Полученная выше оценка находится в очень хорошем согласии с физиологической оценкой разрешающей способности глаза. Оказывается, что размер дифракционного пятна на сетчатке глаза приблизительно равен размеру светочувствительных рецепторов. В этом можно усмотреть мудрость Природы, которая в процессе эволюции стремится реализовать оптимальные свойства живых организмов.
2.4.3. Предел разрешения микроскопа
В случае микроскопа объект располагается вблизи переднего фокуса объектива. Интерес представляет линейный размер деталей объекта, разрешаемых с помощью микроскопа. Изображение, даваемое объективом, располагается на достаточно большом расстоянии L>>F. У стандартных микроскопов L = 16 см, а фокусное расстояние объектива – несколько миллиметров. Объект может располагаться в среде, показатель преломления которой n > 1 (иммерсия).
Радиус пятна Эйри в плоскости изображения равен 1.22lL/D, где D – диаметр объектива. Следовательно, микроскоп позволяет разрешить две близкие точки объекта, находящиеся на расстоянии l, если центры их дифракционных изображений окажутся на расстоянии l', превышающим радиус дифракционного пятна (критерий Рэлея).
![]() (2.7)
(2.7)
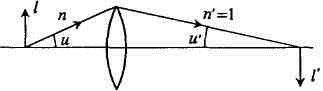 |
Рисунок 2.5.
К условию синусов Аббе.
Чтобы перейти к линейным размерам самого объекта, следует воспользоваться так называемым условием синусов Аббе, которое выполняется для любого объектива микроскопа:
![]() (2.8)
(2.8)
При написании последнего выражения принята во внимание малость угла u'. Отсюда для предела разрешения объектива микроскопа получаем выражение:
![]() (2.9)
(2.9)
Угол 2u называют аппретурным углом, а произведение n*sinu – числовой апертурой. У хороших объективов угол u близок к теоретическому пределу u=p/2. Полагая для примера показатель преломления иммерсионной жидкости n = 1,5, получим оценку: lmin=0,4l.
2.4.4. Замечание о нормальном увеличении оптических инструментов.
Как в телескопе, так и в микроскопе изображение, полученное с помощью объектива, рассматривается глазом через окуляр. Для того, чтобы реализовать полностью разрешающую способность объектива система окуляр–глаз не должна вносить дополнительных дифракционных искажений. Это достигается целесообразным выбором увеличения оптического инструмента (телескопа или микроскопа). При заданном объективе задача сводится к подбору окуляра. На основании общих соображений волновой теории можно сформулировать следующее условие, при котором будет полностью реализована разрешающая способность объектива: диаметр пучка лучей, выходящих из окуляра не должен превышать диаметра зрачка глаза d3p . Таким образом, окуляр оптического инструмента должен быть достаточно короткофокусным.
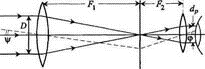 |
Рисунок 2.6.
Телескопический ход лучей
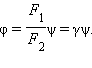 | 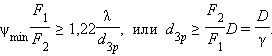 | ||
Здесь g = F1/F2 – угловое увеличение телескопа. Отношение D/g имеет смысл диаметра пучка, выходящего из окуляра. Знак равенства в (4.10) соответствует случаю нормального величения.
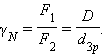 (2.11)
(2.11)
В случае нормального увеличения диаметр пучка лучей, выходящих из окуляра, равен диаметру зрачка d3p . При g>gN в системе телескоп–глаз полностью используется разрешающая способность объектива. Аналогичным образом решается вопрос об увеличении микроскопа. Под увеличением микроскопа понимают отношение углового размера объекта, наблюдаемого через микроскоп, к угловому размеру самого объекта, наблюдаемого невооруженным глазом на расстоянии наилучшего зрения d, которое для нормального глаза полагается равным 25 см. Расчет нормального увеличения микроскопа приводит к выражению:
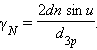 (2.12)
(2.12)
Вывод формулы (2.12) является полезным упражнением для студентов. Как и в случае телескопа, нормальное увеличение микроскопа есть наименьшее увеличение, при котором может быть полностью использована разрешающая способность объектива. Следует подчеркнуть, что применение увеличений больше нормального не может выявить новые детали объекта. Однако, по причинам физиологического характера при работе на пределе разрешения инструмента целесообразно иногда выбирать увеличение, превосходящее нормальное в 2–3 раза.
Перейти на страницу: 1 2 3 4 5 6 7
