Задача о фотоне
Энергия фотона может быть выражена через длину волны ![]() :
:
![]()
Когда фотон взаимодействует «один на один» с электроном, электрон забирает всю энергию фотона, которого с этого мгновения больше не существует. В этом случае говорят, что электрон поглотил фотон.
Излучая фотон, электрон теряет часть своей энергии, которая уносится светом. При этом масса тела согласно формуле Эйнштейна уменьшается. Оказывается, что фотон – это удивительная частица, которая обладает своей энергией ![]() , импульсом
, импульсом ![]() , но не обладает своей массой. Как говорят физики, это безмассовая частица (m=0).
, но не обладает своей массой. Как говорят физики, это безмассовая частица (m=0).
Благодаря Эйнштейну фотон встал в ряд с другими элементарными частицами, только в отличие от них он не имеет массы и «обречен» всегда летать со скоростью света.
3. Разработка алгоритма решения задачи
Энергия фотона может быть выражена через длину волны ![]() :
:
![]()
Когда фотон взаимодействует «один на один» с электроном, электрон забирает всю энергию фотона, которого с этого мгновения больше не существует. В этом случае говорят, что электрон поглотил фотон.
Энергия фотона после соударения со свободным покоящимся электроном может быть выражена через длину волны
![]() :
: ![]() , где
, где ![]()
из (1) следует ![]() , откуда
, откуда 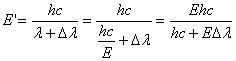 .
.
Исходя из данной формулы, выполнив расчеты, получим значение энергии рассеянного фотона
![]()
![]() – импульс падающего фотона
– импульс падающего фотона
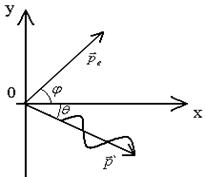
![]() – импульс рассеянного фотона
– импульс рассеянного фотона
![]() – импульс электрона отдачи.
– импульс электрона отдачи.
Из закона сохранения импульсов следует:
Ох: ![]() ;
; ![]() ;
;
Оy: ![]() ;
; ![]() ;
;
Разделим второе выражение на первое, получим:
![]() ;
; 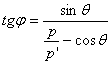
![]() – импульс падающего фотона,
– импульс падающего фотона,
![]() – импульс рассеянного фотона.
– импульс рассеянного фотона.
![]() ,
, ![]()
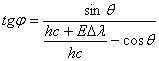
Косинус угла рассеивания ![]() определим, воспользовавшись формулой Комптона.
определим, воспользовавшись формулой Комптона.
![]() , где
, где ![]() – комптоновская длина волны электрона
– комптоновская длина волны электрона
Рассчитаем комптоновскую длину волны электрона ![]()
![]() ;
; ![]() ;
; ![]()
Рассчитаем угол, под которым вылетел электрон отдачи
![]()
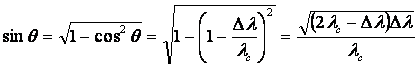
 Итак
Итак 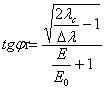 ,
,
откуда 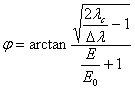 – угол вылета электрона отдачи.
– угол вылета электрона отдачи.
Рассчитаем кинетическую энергию электрона отдачи ![]() , используя следующую формулу.
, используя следующую формулу.
![]()
4. Блок-схема программы
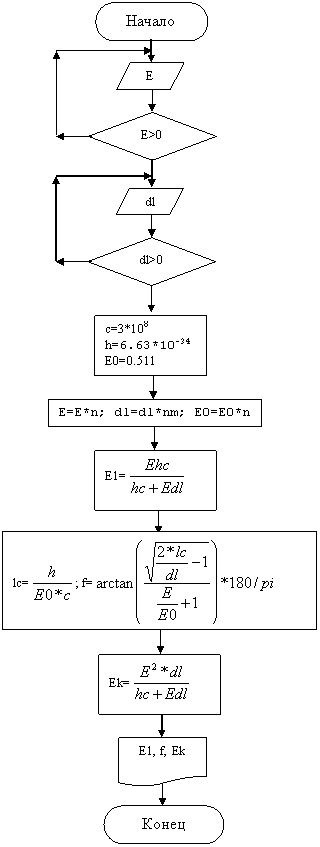
5. Листинг программы
Program Foton;
uses crt;
const n=1.6E-13; {1 Мэв=1.6*10 в -13 степени Дж}
nm=1E-9; {1 нанометр =10 в -9 степени метров}
var E,dl,c,h,e0,Temp:real;
{E - энергия фотона, dl - длина волны, Temp - временная переменная}
{c - скорость света, h - постоянная Планка,e0 - энергия покоя электрона}
lc,E1,f,Ek:real;
{E1 - энергия рассеянного фотона, f - угол вылета электрона
Ek - кинетическая энергия фотона, lc - длина волны в вакууме}
cod:char; {код клавиши}
begin
clrscr; {очистка экрана}
Textcolor(2); {установка цвета символов}
Gotoxy(33,9); {перемещение в позицию с координатами 33,9}
Writeln('КУРСОВАЯ РАБОТА '); {вывод сообщения на экран }
Textcolor(4);
Gotoxy(25,12);
Writeln('Расчет энергии рассеянного фотона,');
Gotoxy(28,13);
Writeln('угла вылета электрона отдачи');
Gotoxy(22,14);
Writeln('и кинетической энергии электрона отдачи');
TextColor(6);
Gotoxy(35,23);
Write('Для продолжения нажмите клавишу <ПРОБЕЛ>');
While cod<>#32 do {пока не нажата клавиша с кодом 32 (ПРОБЕЛ)}
Перейти на страницу: 1 2 3 4 5
