Процессы интермитенсии в ядерных реакциях с большим поперечным импульсом
ПРОЦЕССЫ ИНТЕРМИТЕНСИИ В ЯДЕРНЫХ ВЗАИМОДЕЙСТВИЯХ С БОЛЬШИМ PT
ВВЕДЕНИЕ
Современная физика рассматривает два типа придельных процессов : Гаусовские и не-Гауссовские. Соответственно, мы делим исследуемые проблемы на две ветви. Первый класс включает слабо флуктуирующие процессы. Во втором случае рассматриваются сильно флуктуирующие. Такой подход чрезвычайно полезный и обеспечивает большие возможности для точных решений. Это позволяет получать оптимальные математические модели и решать проблемы количественных исследований, как для слабо флуктуирующих монофазных так и для сильно флуктуирующих многофазных систем. Этого достаточно для физического процесса и математической модели, которая может быть получена на его основании.
Последние годы засвидетельствовали достаточно высокую активность в исследовании сильно флуктуирующих не-Гаусовских процессов, как в теоретическом так и в практическом аспектах. Основная особенность подобных реальных объектов - масштабная инвариантность в все уменьшающихся доменах. Поэтому, первая надежда -что масштабная инвариантность или самоподобность могли бы открыть новые направления, в конечном счете ведущие к более глубокому проникновению в свойства изучаемых событий. Имеются два пути изучения сильно флуктуирующих динамических систем. Первый включает анализ поведения решения для набора дифференциально-разностных уравнений. Второй подход состоит в том, чтобы изучить экспериментальное или теоретическое поведение сильно флуктуирующих динамических переменных (или, возможно, некоторая функция ряда динамических переменных) все время уменьшающихся элементов фазового пространства. В этой работе используется второй путь.
Теория факториальных моментов

Пусть у нас имеется N событий в которых исследуемая величина (h) сильно флуктуирует (Рис.1). Этот процесс может быть описан путем деления соответствующего интервала D на M (для определенности) интервалов величиной
d=D/M (1)
Пусть p1 .pM вероятность нахождения частицы в соответствующем интервале. Флуктуация h описывается вероятностным распределением:
P (p1 . PM) dp1 . dpM (2)
Распределение (2) - сложное многомерное распределение, которое трудно изучать непосредственно. Эта проблема может быть решена путем изучения нормированных моментов этого распределения, определенных как:
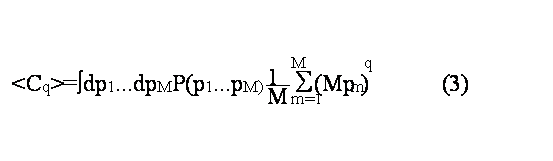
Где последняя часть уравнения - нормирующий член.
Распределение P (p1 . PM) в (2) - теоретическое. Оно не может быть получено из непосредственных измерений. На эксперименте мы имеем дело с распределением величин n1 . nM
 (4)
(4)
Где Q(n1 . nM) измеряемое распределение и П статистический шум (определяемый с помощью распределения Пуассона) который ”размазывает” P (p1 .pM) (теоретическое распределение), особенно для малого числа измерений.
“Динамическая” - в противоположность “статистической” - интерпретация флуктуации получила свое применение в методе факториальных моментов, в котором нормированные факториальные моменты теоретического распределения приравниваются к величинам нормированных факториавльных моментов экспериментального распределения .Этот метод предложили A. Bialas и R. Peschansky.
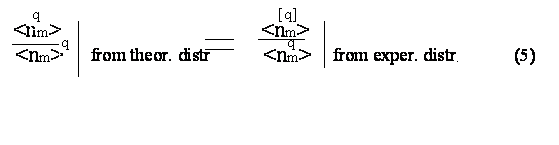
Где ![]()
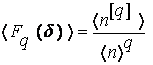 (6)
(6)
В формуле (6) <Fq(d)> факториальный момент, показатель q показывает свойства корреляции порядка q для данного распределения.
На эксперименте распределение изучается для последовательности доменов фазового пространства d путем последовательного деления первоначального интервала D на М равных частей.
d=D/M
Для достижения статистической точности факториальных моментов Fq’ые индивидуальных ячеек определенные в формуле (6) , усреднены по событиям и по М. ячейкам (“ вертикальный анализ ”). Вертикально (по событиям) усредненные моменты могут быть определены как двойное среднее число:
 (7)
(7)
Где nm (m=1, .,M)- множественность того ,бина и
![]() средняя множественность в бине m.
средняя множественность в бине m.
В этой работе мы использовали модифицированный метод вертикального усреднения в котором моменты усреднены по начальным точкам расположения начальной области D.
 (8)
(8)
где Nstep число малых ( step/D << 1 ) шагов расположения начальной точки области D в области пионизации. В качестве основной переменной в этой работе мы используем псевдобыстроту h = - ln tg q/2 вторичных частиц. Первоначальная область D равна 4.0, а M = 40.
Таким образом факториальные моменты выявляют динамические флуктуации и устраняют, или уменьшают насколько это возможно, статистические флуктуации- шум- возникающие из-за ограниченности числа частиц nm в попадающих в исследуемую ячейку m.
Можно показать, что для все время уменьшающихся доменов фазового пространства d вплоть до разрешающей способности, зависимость среднего факториального момента <Fq> от размеров бинов фазового пространства подчиняется степенному закону:
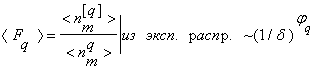 (9)
(9)
для фрактального распределения флуктуаций с перемежающейся вероятностью. Положительная константа j(q) называется показатель интермиттенси. Она характеризует силу эффекта.
Наоборот если рассматриваемое распределение гладкое(плотность вероятности конечная, на пример гаусоподобное распределение)
![]() (10)
(10)
Перейти на страницу: 1 2
