Рефераты по Физике

Простой эффект Джозефсона

Страница 2

Стационарный эффект Джозефсона

Джозефсон рассматривал частный случай туннельного эффекта - туннелирование куперовских пар - и предсказал существование двух эффектов. Первый из них состоит в том, что через туннельный переход с тонким слоем диэлектрика, когда его толщина меньше или порядка длины когерентности $\xi$($d \leq \xi$), возможно протекание сверхпроводящего тока, то есть тока без сопротивления. Предсказывалось, что критическое значение этого тока будет своеобразно зависеть от внешнего магнитного поля. Если ток через такой переход станет больше критического, то переход будет источником высокочастотного электромагнитного излучения. Это нестационарный эффект Джозефсона, который в данной работе не рассматривается

Понадобилось немного времени, чтобы обнаружить эти эффекты экспериментально. Более того, вскоре стало ясно, что эффекты Джозефсона присущи не только туннельным переходам, но и более широкому классу объектов - сверхпроводящим слабым связям, то есть участкам сверхпроводящей цепи, в которых критический ток существенно подавлен, а размер участка порядка длины когерентности $\xi$.

В основе эффектов Джозефсона лежат квантовые свойства сверхпроводящего состояния (см. выше). Действительно, сверхпроводящее состояние характеризуется когерентностью куперовских пар: эти пары электронов находятся на одном квантовом уровне и описываются общей для всех пар волновой функцией, ее амплитудой и фазой. Они когерентны как частицы света - фотоны в излучении лазера, которое также характеризуется амплитудой и фазой электромагнитной волны.

Представим теперь себе два массивных куска одного и того же сверхпроводника, полностью изолированных друг от друга. Так как оба они находятся в сверхпроводящем состоянии, каждый из них будет характеризоваться своей волновой функцией. Поскольку материалы и температуры одинаковы, модули обеих волновых функций должны совпадать, а фазы произвольны. Однако, если установить между ними хотя бы слабый контакт, например туннельный, куперовские пары будут проникать из одного куска в другой и установится фазовая когерентность. Возникнет единая волновая функция всего сверхпроводника, которую можно рассматривать как результат интерференции волновых функций двух половинок. Ниже будет показано, что сверхпроводники со слабыми связями дают уникальную возможность наблюдения фазы волновой функции в макроскопическом масштабе аналогично проявлению фазы электромагнитной волны в явлениях интерференции в оптике.

Следует заметить, что слабая связь между двумя сверхпроводниками - это просто удобный объект для обнаружения интерференционных эффектов. Однако такие эффекты были известны сравнительно давно. Один из ярких примеров - квантование магнитного потока и тока в сверхпроводящем кольце. Действительно, сверхпроводящий ток может принимать только такие значения, при которых на длине кольца может уложиться целое число длин волн волновой функции сверхпроводящих электронов, то есть при обходе по контуру кольца волновая функция в каждой точке попадает в фазу сама с собой. Еще раз видна полная аналогия с квантованием орбит в атоме Бора.

Как уже упоминалось, стационарный эффект Джозефсона состоит в том, что достаточно слабый ток I (меньший критического тока слабой связи Ic) протекает без сопротивления, то есть на ней не происходит падения напряжения. Джозефсон получил следующее выражение для тока I:

$I = I_{c} \sin \varphi$, (1)

где $\varphi$- разность фаз волновых функций по разные стороны слабой связи. В своей работе [Josephson B.D.,1962] Джозефсон предсказал, что в области диэлектрической прослойки будут интерферировать когерентные токи, исходящие из обоих сверхпроводников, так же как световые волны от двух когерентных источников. Поэтому результирующий ток оказывается пропорциональным синусу разности фаз.

Через год после предсказания Джозефсона этот эффект проверил прямым экспериментом Дж. Роуэлл. В туннельных экспериментах такого рода, когда диэлектрическая прослойка очень тонка, основная трудность состоит в устранении контакта металлических обкладок из-за дефектов диэлектрика. Надо каким-то образом доказать, что наблюдаемый ток не является следствием тривиальных закороток, а действительно является туннельным током. Для этого Дж. Роуэлл поместил туннельный переход в магнитное поле, направленное вдоль плоскости барьера. Естественно, что магнитное поле не может влиять на закоротки и в этом случае ток практически не изменился бы. Однако даже очень слабое магнитное поле влияло на ток, причем совершенно нетривиальным образом.

Дело в том, что магнитное поле изменяет фазу волновой функции сверхпроводящих электронов. Поскольку в этом, пожалуй, наиболее ярко проявляется макроскопический квантовый характер сверхпроводящего состояния и эти явления продолжают оставаться в центре внимания и в настоящее время, рассмотрим их более подробно.

Квантовая интерференция

Уже в первом эксперименте было обнаружено, что максимальный сверхпроводящий ток Ic в магнитном поле, параллельном плоскости контакта, немонотонно зависит (с периодом, равным кванту потока $\Phi_{0}$) от величины магнитного потока $\Phi$, проникающего в контакт. Эта зависимость показана на рис. 2. Как видно из рисунка, в случае, когда поток равен целому числу квантов $\Phi_{0}$, происходит компенсация токов, текущих в противоположные стороны в разных точках контакта, и результирующий критический ток оказывается равным нулю. Этот график аналогичен зависимости интенсивности света на экране при дифракции на одиночной щели от расстояния до центральной точки и наглядно демонстрирует волновые свойства сверхпроводящих токов.

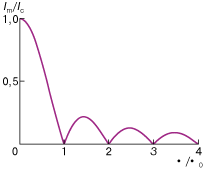
Зависимость критического тока Im

Рис. 2.Зависимость критического тока Im (нормированного на критический ток при отсутствии поля Ic) джозефсоновского контакта от величины потока внешнего магнитного поля

Перейти на страницу:  1  2  3  4