Молекулярно кинетическая теория
Сумма квадратов скоростей движущихся молекул деленная на их число равна квадрату средней квадратичной скорости <c>2 движения молекул, т.е.: 
. (10)
Используя выражение (10), формулу (9) запишем в виде: 
или, учитывая, что (11)
Давление газа р определяется силой, действующей на единицу площади (площадь грани куба с ребром l равна l2).
или, используя формулу (11) запишем: 
. Объем куба V = l3. Такой же объем занимает газ. Поэтому: 
(12)
Формула (12) есть основное уравнение молекулярно-кинетической теории идеального газа для давления. Сделанный вывод для сосуда в форме куба оказывается справедливым для сосуда любой формы.
Уравнение (12) можно записать иначе. Отношение
(число молекул в единице объема или концентрация молекул). Умножим и разделим правую часть равенства (12) на 2. Тогда получим: 
Величина 
- есть средняя кинетическая энергия поступательного движения одной газовой молекулы. Окончательно имеем: 
. (13)
Учитывая, что 
, получим: 
или 
. (14)
Таким образом, формулы (12), (13), (14) выражают основное уравнение молекулярно-кинетической теории идеального газа для давления.
5.Скорости газовых молекул
Формулу (12) можно записать в виде: 
, (15) где 
(масса газа).
Из выражения (15) вычислим среднюю квадратичную скорость движения молекул газа: 
. (16)
Зная, что 
(R-универсальная газовая постоянная;R=8,31 
), получим новые выражения для определения <c>.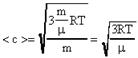 
. (17)
Опытное определение скоростей движения молекул паров серебра впервые был проведен в 1920 г Штерном.
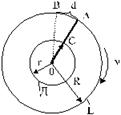Рис. 5
Из стеклянного цилиндра Е выкачивался воздух (рис. 5). Внутри этого цилиндра помещался второй цилиндр Д, имеющий с ним общую ось О. Вдоль образующей цилиндра Д имелся прорез в виде узкой щели С. По оси протягивалась посеребренная платиновая проволока, по которой можно было пропускать ток. При этом проволока раскалялась и серебро с ее поверхности обращалось в пар. Молекулы паров серебра разлетались в различные стороны, часть их проходила через щель С цилиндра Д и на внутренней поверхности цилиндра Е получался налет серебра в виде узкой полоски. На рис. 5 положение полоски серебра отмечено буквой А.
Когда вся система приводилась в очень быстрое движение таким образом, что проволока являлась осью вращения, то полоска А на цилиндре Е получилась смещенной в сторону, т.е. например, не в точке А, а в точке В. Это происходило потому, что пока молекулы серебра пролетали путь СА, точка А цилиндра Е успевала повернуться на расстояние АВ и молекулы серебра попадали не в точку А, а в точку В.
Обозначим величину смещения серебряной полоски АВ = d; радиус цилиндра Е через R, радиус цилиндра Д через r, а число оборотов всей системы в секунду через n
.
За один оборот системы точка А на поверхности цилиндра Е пройдет путь, равный длине окружности 2pR, а за 1 секунду она пройдет путь 
. Время t, в течение которого точка А переместилась на расстояние АВ = d, будет равно: 
. За время t молекулы паров серебра пролетали расстояние CA = R - r. Скорость их движения v может быть найдена, как пройденный путь, деленный на время: 
или, заменяя t, получим: 
.
Налет серебра на стенке цилиндра Д получался размытым, что подтверждало наличие различных скоростей движения молекул Из опыта можно было определить наиболее вероятную скорость vвер которая соответствовала наибольшей толщине налета серебра.
Наиболее вероятную скорость можно рассчитать по формуле, данной Максвеллом: 
. (18) По вычислениям Максвелла средняя арифметическая скорость движения молекул равна: 
. (19)
6.Энергия поступательного движения молекул газа
Кинетическая энергия, которой обладают n молекул газа при некоторой температуре Т вследствие своего поступательного движения равна: 
или 
Так как 
, то 
. (20)
Из основной формулы кинетической теории (12) следует, что 
. (21)
Разделив (20) на (21), получим: 
или 
. (22)
Перейти на страницу: 1 2 3 4 5 6