Явления переноса в жидкостях
Ньютоновская и неньютоновская жидкости
Вязкие тела отличаются от пластичных тем, что текут при любых напряжениях (τ=0). Течение идеально вязких тел (жидкостей) описывается известным законом Ньютона, который в случае сдвига выражается в следующей форме:
= τ =η
, (1)
где f –сила вязкостного сопротивления; η –динамическая вязкость. Закн Ньютона является определением понятия η:
η=
(2)
Понятия «жидкости» и «твёрдый» материал не являются абсолютными и связаны со скоростью деформации. Тем не менее многие структурированные системы низким содержанием дисперсной фазы, характеризующиеся малой прочностью, обладают текучестью, близкой к течению чистых жидкостей. Для изучения особенностей течения подобных систем, как и неструктурированных суспензий и золей, применяют обычный для жидкостей метод капиллярной вискозиметрии, основанный на измерении объёмной скорости течения через капилляр.
Применение закона Ньютона к ламинарному течению в цилиндрическом капилляре или трубке, характеризуемому условием Re<2300 (где Re=ud/ν –критерий Рейнольдса; d –диаметр капилляра; ν –кинематическая вязкость), приводит к формуле Пуазейля
Q=us=πPr
/8ηl=K/η·P (3)
где Q –расход жидкости (поток) в единицу времени; P –давление; r и l –радиус и длинна капилляра; K –константа, определяемая геометрическими параметрами.
Законы Ньютона и Пуазейля применимы для чистых жидкостей и растворов, в том числе и для многих коллоидных систем. Вязкость η дисперсной системы (золя, суспензии) увеличивается с ростом содержания дисперсной фазы. Эта связь выражается законом Эйнштейна
(η -η
)/η=κφ, (4)
где η и η-вязкости коллоидного раствора и чистой дисперсной среды; φ=V
/V –объёмная доля дисперсной фазы (V) в общем объёме системы (V); κ –константа, определяемая формой частиц.
Физический смысл этого закона заключается в том, что относительное приращение вязкости прямо пропорционально относительному содержанию дисперсной фазы. Чем больше φ, тем сильнее выражено тормозящее влияние частиц (не обладающих внутренней текучестью) на поток. Расчёты, проведённые Эйнштейном, показали, что для сферических частиц κ=5/2. В этом случае уравнение (4) может быть записано в следующей форме:
η=η(1+2,5φ). (5)
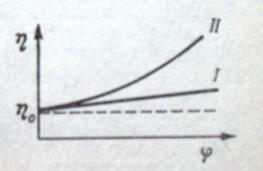Экспериментальные данные для некоторых коллоидных растворов подтверждают линейный характер зависимости η от φ (криваяI); такие жидкости
называются обычными или ньютоновскими жидкостями. В общем случае ньютоновскими называются тела, вязкость которых η не зависит от напряжения сдвига, является постоянным параметром в уравнении (1). Структурированные коллоидные системы отличаются от обычных тем, что не поддаются законам Ньютона,
1
Пуазейля и Эйнштейна. Для низ значение η обычно возрастает с ростом φ значительно сильнее (кривая II), чем это следует из (4).
Тела, вязкость которых непостоянна и является функцией напряжения сдвига в уравнении Ньютона, называются неньютоновскими. Вязкость их так же описывается уравнением (1), но η= η(τ). Для них характерны кривые типа II.
При малых P наблюдается медленное течение с зависимостью Q от P и очень малым наклоном, соответствующим весьма высоким значениям η (3). Анализ этого участка показал, что время перемещения частицы от одного контакта к другому превышает время установления контакта. Связи успевают обратимо восстанавливаться, и течение, таким образом, происходит при совершенно не разрушенной структуре. Это явление называется ползучестью. Для некоторых материалов (например, льда)ползучесть (
) настолько мала, что участок ОА (рис. 2) практически сливается с осью абсцисс и можно говорить о
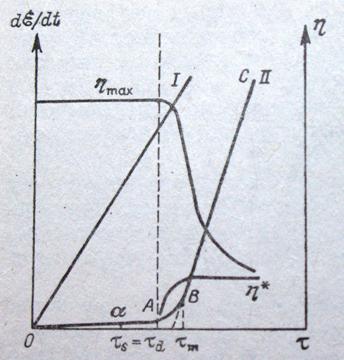предельном статическом напряжении сдвига τ
, ниже которого тело практически не течёт. Эта величина по смыслу близка к пределу упругости τ
, поскольку при τ > τструктурную сетку можно рассматривать как сплошной статический твёрдообразный упругий каркас (матрицу).
Далее с ростом τ начинается постепенное разрушение временных контактов между элементами структуры и и образование других: возникает динамическое равновесие, 
резко возрастает, и для многих пластичных тел реологическая кривая выходит на линейный участок ВС, отражающий нарастающее разрушение структуры. Изучение реологических свойств пластичных тел было впервые проведено выдающимся русским учёным Шведовым (1889г.); закон течения в области разрушения структуры для этих тел (участок ВС)описывается уравнением Шведова –Бингама:
τ= τ
+η*· . (6)
Величина τ(находимая путём экстраполяции прямой ВС на ось τ) называется предельным динамическим напряжением сдвига и характеризует сдвиговую прочность структуры. Постоянная η* носит название пластической вязкости; она учитывает (через η*· = τ - τ) ту часть сопротивления деформации, которая пропорциональна скорости сдвига. Другая часть сопротивления, не зависящая от , учитывается величиной сдвига прочности τ. Напряжение как бы разбивается на две составляющие: необходимые для разрушения структуры (τ) и осуществляющие течение (τ - τ); однако фактически оба процесса осуществляются во времени. Определение τпосредствам экстраполяции отрезка ВС на ось абсцисс количественно характеризует прочность структуры.
Перейти на страницу: 1 2 3 4 5 6