Связанные контура
связанные контура
Содержание
Введение.
Основные понятия.
Контур, эквивалентный связанным контурам. Вносимые сопротивления.
Резонансные характеристики системы двух связанных контуров.
Полоса пропускания системы двух связанных контуров.
Энергетические соотношения в связанных контурах.
Настройка системы двух связанных контуров.
Прохождение радиоимпульса через двухконтурную связанную систему
литература
Введение.
В радиотехнике широкое применение находят всевозможные колебательные контура. Основное назначение радиотехнических колебательных цепей - получение с их помощью частотной избирательности, т.е. выделения полезного сигнала и подавления всех остальных сигналов и помех. Ввиду того что с помощью одиночного колебательного контура нельзя получить высокую избирательность при широкой полосе пропускания, используют связанные контуры. В радиотехнике такие контуры применяются в основном как фильтры промежуточной частоты (ФПЧ).
Основные понятия.
Два контура называются связанными, если колебания, происходящие в одном из них, захватывают другой контур. Связь между контурами может осуществляться через электрическое поле (благодаря емкости) или через магнитное поле (благодаря взаимоиндуктивности или индуктивности). На рис. 1 показаны три разновидности связи двух колебательных контуров: а) трансформаторная, когда связь между контурами осуществляется благодаря взаимоиндуктивности между катушками L1 и L2; б) автотрансформаторная, когда связь между контурами осуществляется непосредственно через индуктивность связи L1,2; в) емкостная, когда связь между контурами осуществляется через емкость связи С3. Наиболее часто в радиотехнике применяется трансформаторная связь, поэтому все дальнейшие выкладки проведем для этого вида связи.
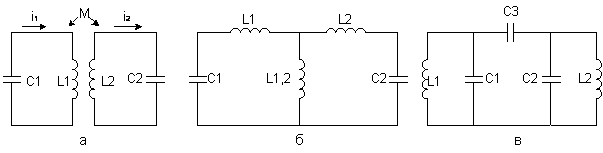
Рис. 1. Виды связи двух колебательных контуров
Предположим, что в первом контуре на рис.1, а протекает ток i1, а второй контур разомкнут. Тогда отношение напряжения, индуцированного в катушке L2, к напряжению в катушке L1 выразится коэффициентом
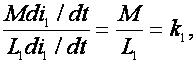
который называется степенью связи. Аналогично, если предположить разомкнутым первый контур, а источник э.д.с. подключить ко второму контуру, то при протекании в нем тока i2 получим
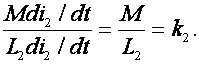
Коэффициент связи есть корень квадратный из произведения степеней связи 
. (1)
При трансформаторной связи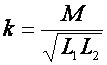 
. (2)
Если умножить числитель и знаменатель (2) на w, то получим общее выражение для коэффициента связи, пригодное и для других видов связи
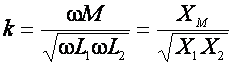(3)
где XM - сопротивление связи.
Контур, эквивалентный связанным контурам. Вносимые сопротивления.
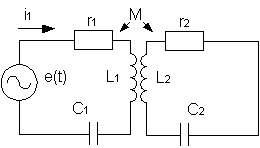
Рассмотрим систему двух колебательных контуров с трансформаторной связью, в которой к первому контуру подключен источник э.д.с. e(t) (рис. 2,а), а r1 и r2 - выделенные для анализа сопротивления потерь в контурах.
а
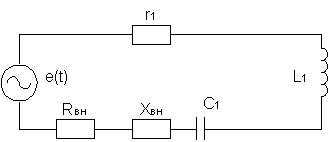
б
Рис.2. Система двух колебательных контуров с трансформаторной связью (а) и ее эквивалентная схема (б)
Запишем для каждого контура уравнения Кирхгофа
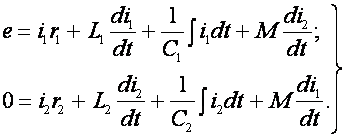(4)
Считая э.д.с. синусоидальной и режим в цепи установившимся, можно воспользоваться символическим методом анализа. Тогда 
; 
и (4) принимает вид
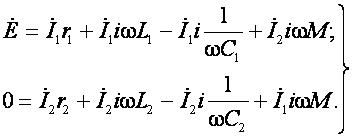(5)
Обозначив реактивное сопротивление первого и второго контуров через X1 и X2, (5) можно записать так:
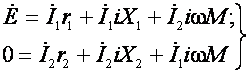(6)
Найдем 
из второго уравнения
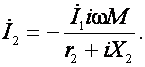(7)
Обозначив wМ = XСВ (сопротивление связи), (7) можно переписать так:
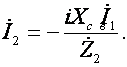
Подставив значение из (7) в первое уравнение системы (6)
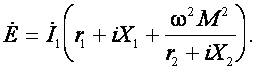
Освободившись от мнимости в знаменателе, получим
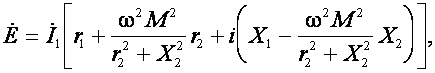
или
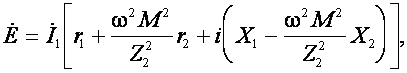
так как 
.
Поделив в полученном выражении приложенную э.д.с. на ток 
запишем выражение для эквивалентного входного сопротивления системы двух связанных колебательных контуров
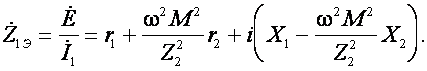(8)
Модуль сопротивления Z1Э равен
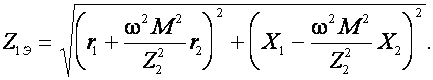(9)
Анализ (8) показывает, что в результате связи первого контура со вторым в первый контур как бы вносятся два сопротивления: активное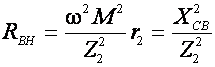 
и реактивное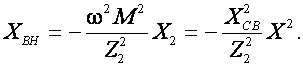 
(10)
Таким образом, систему двух связанных колебательных контуров можно заменить одним эквивалентным контуром (рис. 2, б), в который вносится сопротивление
Перейти на страницу: 1 2 3 4 5