Сверхпроводимость и низкие температуры
Теплоемкость металла складывается из электронной теплоемкости и теплоемкости кристаллической решетки. При низких температурах основной вклад в теплоемкость металла вносит электронная система. Электронная теплоемкость нормального металла соответствует отношению:
 |  | ||
 |
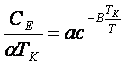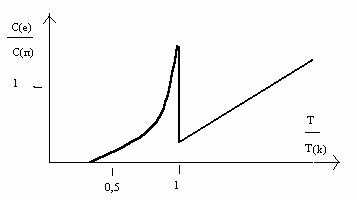Где A и b постоянные, не зависящие от температуры величины. Когда температура сверхпроводника становится равной критической, происходит переход в нормальное состояние и теплоемкость начинает изменяться по линейному закону. Весьма своеобразны свойства теплопроводности в сверхпроводнике. При наличии дифференциального градиента температуры металл не находится в состоянии теплового равновесия. В образце возникает тепловой поток, пропорциональный созданному температурному градиенту. Связь между ними определяется по формуле:
 |
Общий коэффициент теплопроводности складывается из коэффициента теплопроводности электронной системы и коэффициента теплопроводности решетки:
 |
Коэффициент же теплопроводности электронной системы в свою очередь складывается из коэффициента электронной решетки и коэффициента рассеяния примесями.
 |
 |
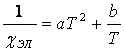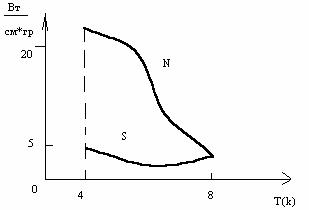Слагаемые в правой части формулы соответствуют χреш, χэл. При переходе металла в сверхпроводящее состояние скачком обращается в нуль сопротивление. Поэтому электронная теплопроводность тоже должна равняться нулю. Тогда при прохождении через критическую температуру должен был бы наблюдаться скачок теплопроводности. Однако этого не происходит. Электронная теплопроводность падает, но остается отличной от нуля.
Для объяснения этого явления была предложена двужидкостная модель. В двужидкостной модели предполагается, что электронную «жидкость» в сверхпроводнике можно представить как совокупность двух жидкостей—нормальной и сверхпроводящей. Нормальная компонента ничем не отличается по своим свойствам от электронной системы нормального образца, сверхпроводящий же—аномален. При повышении температуры количество нормального компонента возрастает, а количество аномального уменьшается и наоборот. В нормальном металле число электронов, участвующих в теплопередаче не меняется в зависимости от температуры, а в сверхпроводящем зависит. Аномальный компонент отвечает за проведение токов, а нормальный—за обычную теплопроводность (χэл) и за рассеивание. Уменьшение числа переносящих энергию носителей естественно приводит к уменьшению χэл.
Решеточную проводимость можно себе представить, как перенос энергии звуковыми квантами—фононами, фононы—это колебания решетки кристалла. Сверхпроводящий переход не меняет состояния кристаллической решетки, однако уменьшение нормальной составляющей, с которой взаимодействуют фононы, осложняет картину—убывание числа фононов сопровождается гораздо более эффективным увеличением длины их свободного пробега, что приводит к росту решеточной теплопроводности. Рост продолжается до тех пор, пока длина пробега не станет больше длины, Обусловленной взаимодействием с примесями и границами кристалла. Тогда последний вид рассеяния начинает играть основную роль, и χреш начинает уменьшаться из-за уменьшения при температурах, близких к абсолютному нулю числа фононов. Сверхпроводимость представляет собой коллективный квантовый эффект кристаллической структуры вещества.
Изотропический эффект
Историческое значение изотропического эффекта во многом состоит именно в том, что он указывал исследователям направление дальнейших поисков по созданию всеобъемлющей теории, объясняющей причину возникновения множества аномалий, которые возникали в веществах, находящихся в сверхпроводящем состоянии.
 |
 |
Перейти на страницу: 1 2 3 4 5 6